Nada más que neuronas...

"The most significant aspect of all this for us is that AlphaGo isn’t just an “expert” system built with hand-crafted rules; instead it uses general machine learning techniques to figure out for itself how to win at Go." (Demis Hassabis, Google DeepMind)

Hoy nos hemos levantado con esta noticia publicada en la famosa revista científica Scientific American: "Computer Beats Go Champion for First Time" (http://www.scientificamerican.com/article/computer-beats-go-champion-for-first-time/)

Esto es un paso más importante de lo que parece a primera vista para la inteligencia artificial. Y es que una red neuronal artificial (imitando el modo en que se cree que funciona la red neuronal de nuestro cerebro), ha conseguido literalmente aprender a jugar al juego Go y vencer a un gran maestro humano. En este juego la fuerza bruta no vale (porque el número de jugadas posibles hace intratable esta técnica: hay más movimientos posibles que átomos en el Universo), y tampoco es posible programar manualmente a priori una larga lista de estrategias de juego ganadoras (como sucede con el ajedrez), así que, sencillamente, el equipo de desarrollo de Google ha necesitado que el sistema aprenda (literalmente) a jugar desde cero como lo hace una persona, a base de practicar una y otra vez.

Cada vez parece más evidente que es sólo la enorme escala a la que funciona nuestra red neuronal cerebral (con trillones de sinapsis) la que consigue producir TODAS nuestras capacidades cognitivas (sin necesitarse nada más), puesto que basta con que nos pongamos a imitar este funcionamiento neuronal (en el caso de este desarrollo del Go "sólo" han necesitado un millón de neuronas artificiales) para que aparezcan maravillosas creaciones en el campo de la inteligencia artificial. En otras palabras; el día que el hardware permita simular ese trillón de sinapsis que se piensa que posee nuestro cerebro, muy probablemente surgirá una conciencia INDIFERENCIABLE de la nuestra (y además ese día puede no estar tan lejos, porque precisamente esto es lo que se propone actualmente un gran proyecto internacional: el proyecto BRAIN). 

Si queréis conocer más detalles técnicos de este proyecto denominado AlphaGo, podéis visitar el blog oficial de Google donde tratan el asunto con mucha más profundidad: https://googleblog.blogspot.com.es/2016/01/alphago-machine-learning-game-go.html 

Por cierto que en marzo de este año, AlphaGo se enfrentará al campeón mundial de Go: Lee Sedol, veremos que sucede ;). 

Os dejo para finalizar un vídeo que han preparado los propios chicos de Google para presentar su logro en este campo de la IA:

Revisión del experimento en favor de la teoría de Jeremy England

"You start with a random clump of atoms, and if you shine light on it for long enough, it should not be so surprising that you get a plant."

Jeremy England (2014), interview commentary with Natalie Wolchover

Hace unos meses terminé de estudiar a fondo el interesante trabajo que el físico Jeremy England está realizando en el MIT (Massachusetts Institute of Technology). En mi blog he divulgado todo lo referente a este trabajo con mucho nivel de detalle, siendo quizás esta entrada el mejor resumen de su teoría.

En un intento de apoyar su propuesta de abiogénesis, realicé un experimento de simulación por computador siguiendo la siguiente propuesta:

1) Programamos un sistema físico que simule lo mejor posible la realidad física.
2) Programamos un modo de calcular la energía del sistema conforme el sistema evoluciona en el tiempo.
3) Procedemos a buscar sistemas complejos mediante computación evolutiva.
4) Calculamos el calor disipado en la formación de tales sistemas ordenados.
5) Estudiamos si existe correlación en esta simulación, entre la complejidad alcanzada y el calor disipado.

Y para reforzar aún más el estudio experimental, procedemos de nuevo, pero sustituyendo el paso 3) y 4) por lo siguiente:

3) Procedemos a buscar sistemas que disipen poco calor mediante computación evolutiva.
4) Calculamos la complejidad del sistema cuando se disipa poco calor.

Si la correlación propuesta entre complejidad y calor disipado es correcta, los sistemas complejos deberán de ir siempre (en la práctica) acompañados de una gran cantidad de calor disipado (energía útil consumida).

¡Y fue precisamente esto lo que he observado cuando he realizado este experimento!

Revisión del código fuente.

Puedes obtener más información sobre este trabajo en el enlace original del artículo que escribí al respecto, pero quiero introducir a continuación la revisión del código fuente que desinteresadamente ha realizado un lector del blog. Carlos Manuel se ha encargado de poner un poco en limpio mi código fuente original, y ha añadido comentarios y algunas nuevas gráficas que clarifican aún más el tema tratado.

Os dejo un enlace al repositorio Git que Carlos ha creado para compartir el programa: https://github.com/CarlosManuelRodr/LennardJones-Evolutivo

Trabajo futuro.

Comentar también, que actualmente estoy trabajando en una nueva versión de este experimento, pero utilizando simulaciones en 3D (en lugar de las 2D del código previo). En cuanto tenga algo consistente escribiré una nueva entrada ;).

Un saludo a todos.

Relación entre mente y computación

“Cuando entendamos el cerebro, la humanidad se entenderá a sí misma” (cita del neurobiólogo Rafael Yuste) 

Se está hablando mucho últimamente sobre la relación entre mente y computación, y me gustaría aportar una reflexión personal que creo os puede interesar. Lo que voy a decir a continuación se basa en este artículo que escribí hace unos meses: http://quevidaesta2010.blogspot.com.es/2015/04/aprendizaje-funcional-automatico.html

Al final del artículo hay una aplicación online donde hice uso de una red neuronal artificial para simular el modo aproximado en que nuestro cerebro aprende probablemente a sumar dos cifras. La cuestión es la siguiente:

Este algoritmo que desarrollé utiliza y simula por computador las bases teóricas en que las neurociencias nos dice que funciona y computa el cerebro: es decir; mediante redes neuronales y potenciales eléctricos. Pues bien, si replicamos esta base teórica (como hice con ese programa en el artículo), vemos que con el equivalente de 20 neuronas (en computación se llaman nodos) y 400 sinapsis bien balanceadas (en computación se llaman enlaces y pesos)  ¡¡se puede generar la capacidad de sumar!!

Indudablemente el hombre es capaz de mucho más que de sumar dos cifras, pero en mi opinión todo es cuestión de escala: si 400 sinapsis bien balanceadas gracias a un proceso de computación evolutiva (leer el artículo completo para más detalle) son capaces de llevar a cabo sumas correctamente en 2 minutos...¡¡que no podrá lograr los trillones de sinapsis que tenemos en nuestro cerebro balanceadas por millones de años de evolución natural!!

Muy probablemente sea únicamente un contraste de escala lo que diferencia los "modestos" avances actuales en IA (usando redes neuronales artificiales) de las capacidades de la mente humana. Pero ya hay grandes proyectos en marcha (por ejemplo, el proyecto BRAIN) que pretenden precisamente una simulación a gran escala del mismo proceso que yo he seguido en mi artículo para simular una red neuronal artificial capaz de aprender a sumar. En el proyecto BRAIN pretenden lograr simular los trillones de sinapsis del cerebro humano (con el balance real), para conseguir (en teoría) que surja de tal simulación unas capacidades equivalentes a las capacidades humanas de un modo casi calcado...en 15 ó 20 años veremos el resultado de este tipo de iniciativas ;).

Es probable que el viejo dilema de "mente sí-mente no" ("o emergentismo sí"-"emergentismo no") quede cerrado definitivamente cuando proyectos tipo BRAIN demuestren que todo es computación neurológica físico-química y ¡nada más!

Un saludo.

Una aplicación útil para la computación evolutiva

Cómo vimos en mi anterior artículo, la computación evolutiva tiene un enorme potencial que, en mi opinión, aún no ha sido suficientemente explotado. Y aunque es cierto que se utiliza con frecuencia para aplicaciones dentro de la inteligencia artificial, su uso podría llegar a ámbitos mucho más diversos. Me gustaría, por lo tanto, aprovechar esta entrada (ahora que ya tenemos una idea de lo que es la computación evolutiva), para mostraros un simple ejemplo práctico que demuestre la gran utilidad que este tipo de procesos computacionales puede tener:

Buscando patrones útiles.

Como ya vimos un ejemplo práctico de computación evolutiva y explicamos su funcionamiento interno, vamos a intentar darle una utilidad práctica a dicho ejemplo. En concreto, el programa de ejemplo era una aproximación numérica a la interpolación de una función desconocida a partir de un conjunto dado de datos.

Vamos por lo tanto a basarnos en esta cualidad del programa, para intentar encontrar patrones desconocidos a partir únicamente de ciertos datos empíricos conocidos. En muchas ocasiones, encontrar este patrón es imposible analíticamente, o si no es imposible, casi siempre es muy laborioso, requiriendo de complejos cálculos.

Un ejemplo de esto que digo puede ser el caso de intentar descubrir el patrón real que hay detrás del crecimiento de la población de un país. En el transcurso de los años, la población no crece o decrece de un modo aleatorio o caótico, sino que, a la vista de los datos, parece seguir cierto patrón o comportamiento. En principio este comportamiento del crecimiento de la población es desconocido, y sólo tenemos los datos empíricos de la población de un conjunto de años (los censos).

Según datos proporcionados por Funk & Wagnalls, el censo de Estados Unidos fue desde 1790 hasta 1990 el siguiente:

Realmente nos gustaría, a partir de estos datos, encontrar cual es el patrón oculto que dirige el crecimiento de la población para así, por ejemplo, poder estimar con cierta seguridad, cual será la población en el 2050 (año para el cual evidentemente aún no tenemos datos xD)

La búsqueda de este patrón es un ejemplo usualmente utilizado en la enseñanza universitaria para explicar al alumnado el concepto de ecuación diferencial. Pero para solucionar algún problema usando ecuaciones diferenciales, primero nos encontramos con el problema de conseguir modelar la situación usando ecuaciones en diferencia, luego nos encontramos con el problema frecuente de buscar el valor adecuado para los posibles parámetros usado en el modelo, y finalmente nos encontramos con el problema de encontrar una solución particular para esa ecuación diferencial a partir de ciertas condiciones iniciales.

Por ejemplo, mediante ecuaciones diferenciales se puede hacer un primer intento de modelado del patrón detrás del crecimiento de la población como este:

Este primer intento de modelo es fácil de calcular, y tiene, como solución analítica:

P(t) = 3.9 * e^(0.003067*t) 

pero cuando se contrasta esta función con los datos, vemos que el error cometido es grande a partir de cierto valor, por lo que finalmente no es un modelo que satisfaga el patrón oculto al crecimiento de la población.

¿Qué hacemos entonces? Pues buscar un nuevo modelo, solucionarlo y comprobar su nivel de aproximación con los datos.

Para este problema concreto, se suele utilizar un modelo llamado modelo logístico de la población, que viene a ser como el anterior, simplemente añadiendo un nuevo parámetro N que hace referencia a la capacidad de soporte del medio. De este modo, el modelo revisado es:

Esta ecuación diferencial ya no es lineal, y su resolución es más compleja, además de que ahora debemos conjeturar el valor de un nuevo parámetro N (además de k).

Este modo de actuar por ensayo y error de modelos es bastante complejo, laborioso y pesado. Para muchos problemas puede ser incluso un método inviable de actuación.

Resolución evolutiva.

¿Qué tal un método sencillo y universal? Un método que no requiera ni siquiera saber qué es una ecuación diferencial y que no necesite que tengamos que conjeturar con modelos para cada problema particular. Este método existe, y consiste simplemente, como seguro ya habréis podido imaginar, en el uso de un algoritmo de computación evolutiva.

La cuestión se reduce de este modo a introducir los datos empíricos en el programa, y a esperar a que el proceso evolutivo encuentre la función que mejor aproxime cada punto. Una vez alcanzada tal función con el nivel de aproximación especificado a priori, podemos estar seguro de que será una buena aproximación al patrón oculto a los datos empíricos de partida.

Posteriormente, simplemente tenemos que probar el patrón alcanzado con datos conocidos pero no pasados al programa (para asegurarnos de su fiabilidad), y finalmente, si la fiabilidad es buena, realizar predicciones para situaciones desconocidas utilizando este patrón hallado.

Aplicación práctica real al caso de estudio del crecimiento de la población de Estados Unidos.

Vamos a hacer uso de la aplicación que desarrollé para el artículo anterior. Como datos de entrada, vamos a introducir los datos facilitados por Funk & Wagnalls del censo de Estados Unidos desde 1790. Para poder estudiar la fiabilidad, no incluiremos las décadas posteriores a 1990. Por lo tanto la entrada del programa quedaría así:

{"x": 0} = 3.9;{"x": 10} = 5.3; {"x": 20} = 7.2; {"x": 30} = 9.6; {"x": 40} = 12;{"x": 50} = 17; {"x": 60} = 23; {"x": 70} = 31;{"x": 80} = 38;{"x": 90} = 50;{"x": 100} = 62;{"x": 110} = 75;{"x": 120} = 91;{"x": 130} = 105;{"x": 140} = 150;{"x": 150} = 131;{"x": 160} = 151;{"x": 170} = 179;{"x": 180} = 203;{"x": 190} = 226;{"x": 200} = 249;error_max = 10

Pulsamos en el botón "Ejecutar el proceso evolutivo" y esperamos las generaciones necesarias hasta que el error de interpolación de los puntos sea inferior a 10.

Cuando yo hice la prueba, el proceso terminó tras 271 generaciones, y me ofreció la siguiente función como resultado:

Es una función intimidante, ¿verdad? No te preocupes, es solo que el proceso evolutivo no busca, como puede hacer el científico humano, la sencillez algebraica. No la necesita. Y por eso esta función nos puede parecer extraña y difícil de entender. Pero es que realmente no necesitamos "comprender" el patrón encontrado, sino simplemente utilizarlo para realizar predicciones fiables con él.

Quizás este resultado sea después de todo una solución particular (o una aproximación) para el modelo logístico de la población que vimos antes, con un par de parámetros k y N desconocidos. O quizás no lo sea. No lo sabemos, pero tampoco lo necesitamos saber. Basta con que el patrón sea fiable.

¿El modelo encontrado es fiable?

Vamos a comprobarlo mediante su contrastación con otros datos conocidos pero que no han sido facilitados al programa.

El valor para las décadas posteriores a 1990 no fue facilitado precisamente con este propósito.

Pero primero veamos como se ajusta la función hallada a los datos facilitados al programa:

Año 1830 (t = 40): Valor predicho: 11,973 millones, Valor real: 12 millones, Error: 0,027
Año 1920 (t = 130): Valor predicho: 105,169 millones, Valor real: 105 millones, Error: 0,169
Año 1960 (t = 170): Valor predicho: 178,937 millones, Valor real: 179 millones, Error: 0,063

Se puede comprobar que existe un ajuste extraordinario.

Veamos, a continuación, cómo se ajusta la función a datos no facilitados al programa, pero que son conocidos empíricamente por otros medios. Como la tabla facilitada por Funk & Wagnalls no ofrece más información, usaremos otra fuente de datos alternativa. En concreto, vamos a usar los valores censales de Estados Unidos ofrecidos por la siguiente página web: http://www.datosmacro.com/demografia/poblacion/usa

Tenemos que tener en cuenta, sin embargo, un factor de corrección entre los datos facilitados por Funk & Wagnalls y los ofrecidos por la página web. Existe una variación entre las fuentes de datos de alrededor de un par de millones de habitantes de media. Por lo tanto, cuando usemos nuestra función para comprobar su fiabilidad con los datos de la web, debemos tener en cuenta estos 2 millones de diferencia (al alza o a la baja) entre losestimado por la función y el dato empírico ofrecido por la web datosmacro.

Teniendo esto en cuenta, hacemos las siguientes pruebas con datos no proporcionados al programa:

Año 1975 (t = 185): Valor predicho: 215,206, Valor real: 215,973 +- 2, Error: -0,767 +- 2
Año 1985 (t = 195): Valor predicho: 241,201, Valor real: 238,410 +- 2, Error: 2,791 +- 2
Año 1995 (t = 205): Valor predicho: 263,933, Valor real: 266,458 +- 2, Error: 2,525 +- 2
Año 2000 (t = 210): Valor predicho: 277,575, Valor real: 282,296 +- 2, Error: 4,721 +- 2
Año 2005 (t = 215): Valor predicho: 291,481, Valor real: 296,115 +- 2, Error: -4,634 +- 2
Año 2010 (t = 220): Valor predicho: 303,252, Valor real: 309,761 +- 2, Error: -6,509 +- 2
Año 2015 (t = 225): Valor predicho: 317,500, Valor real: 319,047 +- 2, Error: -1,547 +- 2

Teniendo en cuenta que gran parte del error cometido es probable que se deba al desajuste entre los datos de Funk & Wagnalls y los datos de la web, posiblemente el error medio cometido por la función cuando se contrasta con datos no usados en el proceso de interpolación esté alrededor de entre uno o dos millones. Este error medio, cuando hablamos de cientos de millones de personas, es bastante aceptable, y nos ayuda sin duda a hacernos una idea bastante ajustada de la población de Estados Unidos en cualquier año pasado o futuro (en el futuro será útil siempre que alguna catástrofe muy acusada no modifique el patrón seguido por el crecimiento real hasta ahora).

Predicciones futuras según el modelo.

¿Qué nos deparan las futuras décadas en cuanto a crecimiento de población en Estados Unidos se refiere? Pues, como digo, si no ocurren catástrofes apocalípticas no contempladas por el proceso tales como una epidemia o una guerra nuclear que aniquile a una gran parte de la población (modificando por lo tanto radicalmente el patrón real subyacente), el número de habitantes será con bastante seguridad el siguiente (con un error probable de un par de millones hacia arriba o abajo):

Año 2020 (t = 230): 332,981 millones de habitantes.
Año 2030 (t = 240): 354,429 millones de habitantes.
Año 2040 (t = 250): 387,272 millones de habitantes.
Año 2050 (t = 260): 425,315 millones de habitantes.
Año 2100 (t = 290): 526,467 millones de habitantes.
Año 2500 (t = 690): 3071,513 millones de habitantes.

Dentro de 5 años (ahora mismo estamos en el 2015), podremos comprobar la primera previsión y ver qué error cometió la estimación de nuestro modelo hallado ;).

Si se mantiene el patrón real seguido por Estados Unidos hasta ahora, vemos que pasarán muchas décadas antes de que alcance los 1000 millones de habitantes que tiene China hoy día.

Resumen.

Hemos visto un nuevo ejemplo del potencial que guarda la computación evolutiva. En este caso, hemos estudiado como ofrece una capacidad asombrosa en el descubrimiento de patrones ocultos; patrones que pueden ser demasiado complejos o caóticos para un estudio tradicional, pero que son perfectamente abordables mediante esta interesante y útil técnica de computación.

¿Qué es la computación evolutiva?

En esta entrada, que ya aviso que será un poco técnica, voy a intentar acercaros la base de lo que es una magnífica herramienta para la resolución de problemas de diversa índole. Me refiero, como no, a la computación evolutiva: la rama de la computación que hace uso del mismo proceso que la naturaleza ha seguido para conseguir fenómenos asombrosos que de otro modo serían totalmente inviables de alcanzar en un tiempo razonable. Por cierto, que gran parte de la moderna inteligencia artificial se basa en este precepto.

Introducción

Entendemos por un algoritmo evolutivo, aquel cuya técnica resolutiva se inspira en la evolución biológica de la naturaleza; imitando de esa manera, el proceso de selección natural que, desde Darwin, es aceptado como el principal motor del proceso evolutivo de los seres vivos.
Existe en la red abundante información teórica al respecto de la computación evolutiva, pero en muy pocos casos me he encontrado con ejemplos prácticos concretos, donde se pongan en práctica dichos principios.

De manera que me he propuesto intentar poner mi granito de arena práctico en esta rama tan interesante de la inteligencia artificial para ayudar así a cualquiera que quiera adentrarse en la materia.

Composición y funcionamiento de un algoritmo evolutivo (AE)

Sin duda, el mejor recurso bibliográfico para iniciarse en el mundo de la CE -compuactión evolutiva- es el magnífico libro Introduction to Evolutionary Computing, de los autores Agoston E. Eiben, y J.E. Smith.

Hemos dicho que la computación evolutiva es una ciencia computacional en la que sus algoritmos imitan el proceso evolutivo de la naturaleza. Veamos de qué partes consta, y cómo funcionan:

Cualquier AE seguirá el siguiente pseudocódigo:



Existe una población de n individuos, los cuales expresan una posible solución. La población es pues, un multiconjunto de genotipos, y forman la unidad de evolución.

Los individuos de la población se van renovando en sucesivas generaciones, que van convergiendo evolutivamente hacia la meta deseada, que no es otra que encontrar una solución a un problema determinado. La evolución se produce durante el paso de las generaciones, y cada generación cumple con el siguiente procedimiento:

La primera generación es especial, y sólo consiste en la generación (y evaluación) de una población inicial de n individuos, normalmente generados aleatoriamente.

El resto de generaciones comienzan con la selección de los individuos que se van a reproducir. Es decir, se seleccionan los padres que conformarán la descendencia.
Y dicha descendencia, será el resultado de un proceso de recombinación y mutación de esos padres previamente seleccionados. Tras la creación de la descendencia, se procede a evaluar su adaptabilidad. Es decir; se calcula, lo bien o mal que se adapta el nuevo individuo a las condiciones del medio ambiente. Este proceso se suele realizar, mediante el uso de una funcion de desempeño (fitness function). Dicha función representará la adaptabilidad del fenotivo expresado por el genotipo en cuestión. Una vez evaluada la progenie, se procede a seleccionar los individuos que finalmente prevalecerán para formar la siguiente generación.

Todo este proceso generacional, se repetirá mientras no se cumpla una condición de parada. La condición de parada normalmente será, o bien que uno o varios genomas expresan un fenotipo que es solución óptima del problema a resolver, o que se alcanzó el máximo de generaciones previstos programáticamente.

A continuación tenéis el programa con el que pondremos en práctica estas ideas. Podéis trastear un poco con él, y más tarde estudiar la explicación técnica del mismo:

Ejemplo VIII:

Podéis descargar el código fuente del ejemplo desde este enlace.

El algoritmo está escrito completamente en Javascript, utilizando hilos mediante la nueva clase Worker nativa de HTML5 (puedes descargar el código fuente desde el enlace de arriba):

Manual de uso

Mediante el algoritmo del ejemplo, vamos a intentar encontrar la solución óptima -si existe-, o la mejor aproximación posible, al siguiente problema:

Tenemos como entrada (inputs), una serie de puntos definidos para ciertos valores de una variable, y queremos buscar la función de interpolación que sea óptima -que pase por todos los puntos dados como entrada- o lo más aproximada posible.

Para introducir los inputs en el programa, debemos rellenar el campo de texto "Datos de interpolación", añadiendo cuantos puntos deseemos. Una entrada válida sería, por ejemplo:

{"x": 0} = 0;{"x": 1} = 3; {"x": 2} = 5.4142;{"x": 3} = 7.732;error_max = 0.001

Si ahora, pulsamos sobre el botón Ejecutar el proceso evolutivo, el programa se iniciará, buscando una de las muchas funciones que interpolan esos puntos, por ejemplo:

f(x) = 2*x + sqrt(x)

Para recalcar la potencia del proceso evolutivo por selección, se propone la posibilidad de intentar encontrar la solución, sin realizar la recombinación, mutación y selección de los más aptos, lo que resulta en un algoritmo completamente aleatorio que muy poco probablemente llegará a solucionar el problema.

Es importante señalar, que sólo se permite los operadores + - * /^, y que la prioridad de los mismos es la tradicional. Se permiten números con decimales (con el punto como separador, y una precisión máxima de cuatro decimales).

Al finalizar la ejecución del algoritmo, aparecerá una nueva zona en la aplicación con un par de gráficas, la primera representando los puntos de interpolación, y una segunda con los puntos representados por la función encontrada por el programa. Ambas gráficas coincidirán siempre y cuando se encuentre una solución óptima -si es que existe-.

Análisis del algoritmo

La representación del genotipo en nuestro ejemplo, consiste en un array de caracteres, conformando una cadena de texto, con los siguientes símbolos permitidos:{[0-9],x,+,-,/,*,^,sin,cos,sqrt,log}

Además, los símbolos deben respetar un patrón que forme cadenas con sentido aritmético (pero no se permite usar el símbolo - como operador unitario), permitiéndose genotipos como 2*x*x-1/2*x+23, pero no otros como 2+-x/*.

El AE del ejemplo responde al siguiente pseudocódigo:


t <- 0
Inicialización P(t)
Evaluación P(t)
hacer
S <- Seleccion_padres[P(t)]
Q = Operacion_variación[S]
Evaluación[Q)]
P(t+1) <- selección[P(t) U Q]
t <- t + 1
mientras no condición de parada


donde S, Q, y P son poblaciones de individuos, y t es una variable de tipo entera.

El algoritmo comienza creando aleatoriamente una población P de n individuos, y evaluando la función de desempeño de sus individuos -lo cerca o lejos que están de ser una solución óptima al problema-.

Posteriormente se entra en un bucle del que sólo se saldrá cuando se cumpla que, o bien en la población P(t) hay un individuo que es solución óptima, o bien se ha llegado al máximo de iteraciones previsto en la configuración del programa.

Cada iteración del bucle, se va a corresponder con una nueva generación de individuos, formada por parte de los padres de la generación anterior y por parte de su progenie.

Para realizar una generación se procede como sigue:

1) Se forma una población S con los individuos que van a poder procrear. En el caso concreto de mi ejemplo, todos los miembros de la población P van a tener descendencia. Es decir; S = P(t).

2) Se procede a crear la descendencia mediante recombinación, y mutación. En el ejemplo, se van seleccionando pares de individuos de S y se recombinan dando lugar a cuatro hijos.

Para recombinar, seleccionamos al padre y lo dividimos por un punto aleatorio p (quedando el padre partido en dos partes: padre1 y padre2). Hacemos lo mismo con la madre en un punto p', y se crean los hijos de la siguiente manera:

h1 = padre1 + madre2
h2 = madre1 + padre2
h3 = padre1
h4 = padre2

Posteriormente, cada hijo, sufrirá -con 100% de probabilidad- algún tipo de mutación puntual, que podrá ser más o menos leve, y que podrá modificar algún valor concreto del genotipo del individuo, o añadir o eliminar partes del mismo.

El proceso de reproducción, se repetirá 16 veces por cada par de padres, lo que dará un total de n*16*4 hijos en cada generación -siendo n el número de individuos en la población-.

3) El siguiente paso es evaluar la adaptabilidad de esta población Q que conforman la nueva descendencia.

4) Por último, se procede a seleccionar aquellos individuos que mejor se adaptan al medio de la unión del conjunto de padres de la generación anterior P(t) y el conjunto de sus hijos Q. Como resultado, se obtiene el conjunto P de la generación siguiente, con los supervivientes del proceso de selección.

En nuestro ejemplo, la evaluación de un genotipo se procesa mediante la aplicación de una función de desempeño (fitness function) al mismo. En este caso, la función será el resultado de sumar la diferencia en valor absoluto entre g(x) y el input en dicho punto: abs(y-g(x)).

Un genotipo óptimo, será aquel cuya función de desempeño tenga valor 0.

Para el AE del ejemplo, la selección generacional, se hace ordenando los individuos de [P(t) U Q] según su valor de adaptación -cuanto menos diferencia entre g(x) y los puntos de interpolación mejor- y seleccionando los s primeros, desechándose de esa manera el resto.

Resumen

El algoritmo evolutivo propuesto es capaz de encontrar; si existe, una solución óptima al problema con bastante frecuencia, aunque; como en todo AE existe la posibilidad de que la evolución generacional se localice en torno a una solución local no óptima -pero muy cercana de serlo-. Sin embargo, la aleatoriedad de la fase de mutación, permite teóricamente recomenzar un nuevo camino evolutivo en cualquier momento -aunque es menos probable que esto ocurra conforme pasan las generaciones-.

Aprendizaje funcional automático

Hace poco, mi hija comenzó en el colegio a aprender a realizar sumas de una cifra. Me resultó muy interesante observar el proceso que siguió para conseguirlo: ni más ni menos que un refuerzo paulatino de aprendizaje por ensayo y error. Esto me recordó un ejemplo de aprendizaje automático por ordenador que realicé hace ya años, y me propuse hacer algo similar adecuándolo al modo en que parece que mi hija ha conseguido aprender a sumar. El resultado lo tenéis a continuación.

Simulando los procesos neurológicos:

El campo más prometedor en IA desde hace décadas, es la simulación neuronal del cerebro animal mediante redes neuronales artificiales. Mediante esta simulación se han conseguido los avances más espectaculares en el terreno de la inteligencia artificial. Baste nombrar uno de los avances más notorios conseguidos por un equipo de desarrollo de Google, donde han conseguido que una única red neuronal artificial sea capaz de aprender de manera autónoma a jugar a 43 juegos diferentes y con un nivel de habilidad mayor al alcanzado por la media de personas. La red neuronal recibe como entrada únicamente los píxeles de colores de la pantalla del juego, y resuelve el modo en que hay que pulsar los distintos botones del mando para jugar bien.

Si este algoritmo se implantase en un robot con una cámara visual, y con "dedos" capaces de manipular un mando de videojuego, tendríamos el equivalente de un chaval jugando (de hecho, en realidad el robot jugaría a esos 43 juegos mejor que la media de chavales).

¿Y cómo se ha conseguido esta hazaña? Pues simplemente simulando por ordenador el funcionamiento de las neuronas del cerebro animal. Se crean nodos artificiales, que son el equivalente a las neuronas biológicas, y se unen unos con otros mediante enlaces o pesos wij (que son el equivalente a las interconexiones sinápticas entre neuronas naturales). Al igual que las neuronas, los nodos artificiales poseen un umbral de activación y un nivel de transmisión o inhibición similar al voltaje que una neurona emite y transmite mediante las dendritas.

Y aunque parezca ser una simulación complicada, en realidad computacionalmente es algo muy sencillo de hacer...¡y funciona!

Reforzando la red neuronal:

Una red neuronal artificial por sí sola no sirve de gran cosa. Si sus pesos y valores de umbral y transmisión contienen cualquier valor posible, la salida que produzca será aleatoria y sin sentido. no será funcional. Es necesario reforzar o entrenar esta red, de modo que se puedan ajustar los pesos y umbrales del modo adecuado para que la red neuronal pueda realizar una función útil.

Existen varios modos de ajustar una red neuronal, pero sin duda la más eficiente y sencilla, al menos en mi opinión, es mediante el uso de un proceso evolutivo.

Simplemente se trata de poner a prueba un gran conjunto de redes neuronales similares, y de ir seleccionando aquellas que mejor aproximen el resultado deseado. En cada generación se crearán nuevas redes a partir de las anteriores, las cuales podrán sufrir leves variaciones en sus parámetros (mutaciones). Esta simple iteración permite ajustar cualquier red neuronal de un modo eficiente para conseguir el fin deseado.

¿Aprendemos nosotros de un modo parecido?:

Tras estudiar el modo en que mi hija aprendió a sumar, yo creo, sin duda, que siguió un esquema muy similar al indicado arriba. Personalmente, creo que una gran parte (si no todo) del aprendizaje no instintivo que consiguen los animales (ser humano incluido), sigue un proceso de refuerzo por ensayo y error sobre un conjunto concreto de neuronas de nuestro cerebro.

Durante millones de años, el proceso evolutivo biológico habría sentado la base neuronal y la plasticidad necesaria para ajustar partes independientes de la masa neuronal para poder, literalmente, reforzar o inhibir las interconexiones y los umbrales de las neuronas de modo que se puedan conseguir salidas funcionales parciales. De este modo, el cerebro sería capaz de poseer cientos de miles de heurísticos (algoritmos) independientes pero conectados, los cuales darían lugar a toda la conducta en su complejidad.

El proceso de aprendizaje (aproximado y simplificado) que probablemente siguió mi hija pudo ser el siguiente:

Los números llegaron a su cerebro en forma de impulsos eléctricos gracias al sentido de la vista. Posiblemente algún heurístico innato (o varios) convirtieron y separaron esos impulsos en entradas para un determinado subconjunto neuronal concreto, el cual produjo una salida que otros heurísticos transformaron en un acto conductual: escribiendo la salida en un papel o diciendo en voz alta la respuesta. Cuando la respuesta fue correcta, nuestra aprobación (o la del profesor) llegó a su cerebro en forma de refuerzo positivo mediante los sentidos de la vista y el oído, y el subconjunto neuronal que se encargó de la tarea se vio reforzado. Cuando la respuesta fue errónea, le indicamos cual era la solución correcta, la cual llegó también a su cerebro y alteró a continuación el ajuste del subconjunto neuronal implicado en este asunto. En el momento que la salida del subconjunto fue  ya siempre correcta, no se recibieron nuevas correcciones, y el aprendizaje habría terminado.

Un nuevo heurístico ha aparecido en el cerebro de mi niña: ahora ya es capaz de sumar :).

El movimiento se demuestra andando:

Como es habitual, no me voy a quedar en la simple teoría, y voy a poner en práctica todo lo dicho mediante un ejemplo que yo mismo he desarrollado, y que podréis probar a continuación desde vuestro propio navegador:

Mediante un proceso de computación evolutiva, veremos como una red neuronal artificial de sólo 40 nodos, es capaz de aprender de manera autónoma a realizar sumas de una cifra (el aprendizaje es autónomo en el sentido de que en ningún momento al algoritmo se le indica cómo hay que sumar, y ni siquiera se le pasan los números en formato decimal. Tampoco se ajusta manualmente en modo alguno las variables de la red neuronal).

Técnicamente hablando, he utilizado una red neuronal con conexión hacia delante y una capa oculta (hidden layer). La capa de entrada contiene 20 nodos que se inicializan a 1 ó 0 según sea el input de entrada (el par de números a sumar). Cada nodo de la capa de entrada se une a cada nodo de la capa intermedia (la cual consta de otros 20 nodos), lo que da un total de 400 enlaces (pesos wij). Un último nodo de salida es el responsable de devolver el resultado del proceso neuronal expresando con su nivel de activación el resultado de la suma .

Inicialmente, los pesos wij de la red neuronal son marcados aleatoriamente, por lo que la respuesta de la red neuronal ante el problema será también aleatoria y casi siempre errónea. Hay pues que entrenar la red para que aprenda a evaluar bien la entrada, lo que vamos a conseguir ajustando evolutivamente los pesos de la red neuronal utilizada, el umbral de activación de cada nodo, y el nivel de transmisicón o inhibición asociado. Dicho entrenamiento evolutivo se realizará mediante una estrategia evolutiva.

Comenzamos con una población de 750 redes neuronales aleatorias (n = 750 individuos). Cada generación producirá n nuevos individuos que podrán sufrir una variación exclusiva por mutación -sin recombinación- y cuya función de desempeño (fitness fuction) será calculada mediante competición -selección por torneo-. Para el proceso de mutación, hay que tener en cuenta que cada individuo; además de un vector de pesos, contiene un vector de variables de ajuste (umbral de activación y valor de transmisión), que también irá evolucionando junto con los pesos. La mutación es de la forma:

Con alpha igual 0.2f, y donde xi indica el peso en la posición i del vector de pesos, y N(0,1) indica un valor tomado aleatoriamente de una distribución normal de desviación típica igual a 1, y media igual a 0. La otra variable que interviene en el proceso se corresponde con la variable de ajuste del elemento i, que; como se puede ver, muta antes de que lo haga el peso xi. La evaluación de un individuo se realiza mediante q pruebas (con q = 100) en donde se comprueba la capacidad del individuo para resolver las 100 combinaciones posibles en que se pueden sumar dos números en el dominio [0-9]. En el paso final de cada generación, se seleccionan aquellos n individuos que mejor han aproximado su respuesta ante las q sumas.

A continuación podéis probar este ejemplo de computación evolutiva que he desarrollado. Para alcanzar un aprendizaje completo, ajusta el campo "Número de generaciones para el aprendizaje" al menos en 150, en lugar de 50 como lo he puesto por defecto. Con el botón "Realizar prueba" podrás probar la funcionalidad de la mejor red neuronal alcanzada tras finalizar el proceso evolutivo:



Podéis descargar el código fuente del ejemplo desde este enlace.

El poder del proceso evolutivo:

Es interesante notar la enorme eficiencia y capacidad que tiene la computación evolutiva para encontrar, dentro de un gigantesco conjunto de posibilidades, los valores adecuados para conseguir un fin concreto. En este ejemplo que estamos estudiando, las combinaciones y los valores posibles para los pesos wij de los 400 enlaces, así como para los umbrales de activación y los valores de transmisión son astronómicos. Para que un proceso aleatorio consiguiese ajustar finamente estos valores de modo que la red neuronal pudiese sumar correctamente, probablemente harían falta cientos de miles de años, y sin embargo, el algoritmo evolutivo lo consigue en unos pocos minutos.

Evidencia a favor de la teoría de Jeremy England (II)

"You start with a random clump of atoms, and if you shine light on it for long enough, it should not be so surprising that you get a plant."

Jeremy England (2014), interview commentary with Natalie Wolchover

Esta entrada es una continuación del estudio práctico que realicé hace unas semanas, del interesante trabajo teórico que el físico Jeremy England está realizando en el MIT (Massachusetts Institute of Technology).

La propuesta teórica viene a decir  que, una (en principio improbable) complejidad estructural, puede prevalecer sobre el caos con tal de que la estructura en cuestión posea la cualidad de disipar mucho calor (consumir mucha más energía que la media).

Esto abre las puertas a la posibilidad de una adaptación espontánea natural hacia la complejidad si se dan unas condiciones adecuadas. Adaptación natural que sería la causa primera de todo proceso evolutivo (incluida la evolución biológica). De hecho, la biología aparecería cuando el grado de complejidad alcanzado por esta adaptación física gradual alcanza cierto umbral.

 La cuestión es que Jeremy deduce todo esto matemáticamente a partir de una física ya establecida (termodinámica y mecánica estadística), pero no aporta pruebas experimentales sólidas de ningún tipo (se limita a hacer alguna propuesta muy vaga y a señalar que su trabajo puede ser corroborado en el futuro). Yo he visto la posibilidad de conseguir una evidencia a favor de su teoría mediante la simulación física por ordenador, y es lo que estoy haciendo estos días.

La explicación en sí es compleja, y podéis entrar más en detalle en mi anterior artículo sobre el asunto, pero valga decir que he logrado realizar un experimento (con una simulación física muy aproximada), que correlaciona completamente con la propuesta de base en la teoría de Jeremy, la cual afirma que: a más complejidad estructural más energía se requiere consumir. Si el consumo baja, la complejidad baja; y si el consumo se mantiene la complejidad se mantiene (¡existe una especie de proceso adaptativo físico y espontáneo en las leyes del universo!) . Esto es un fuerte respaldo para la abiogénesis, y es todo lo que yo personalmente necesito para convencerme de una vez por todas de que la biología aparece a partir de la materia inerte. Y no sólo eso, sino que se puede deducir que la vida es un fenómeno que sólo requiere del tiempo y la oportunidad necesaria para aparecer: la vida sería de este modo un fenómeno inevitable (dada la inmensidad del universo, es seguro que la oportunidad necesaria se dará por doquier, ya que las condiciones no son demasiado estrictas: un sistema abierto y lejos del equilibrio térmico, una fuente continua de energía externa que entra en el sistema, y un baño térmico donde disipar el calor generado tras realizar trabajo físico: huelga decir que estas condiciones se dan en la Tierra desde hace millones de años, tiempo suficiente para que ciertas estructuras aprovechasen la oportunidad para iniciar esta carrera adaptativa espontánea en favor de la disipación de calor y la complejidad).

Por último, recordar que todo esto es importante por otra razón: todos los fenómenos complejos que observamos (absolutamente todos), deben estar supeditado a esta física subyacente: por lo que, desde el movimiento de una bacteria hasta la conducta humana más compleja y abstracta, tiene su origen y su finalidad en la necesidad de consumir energía en forma de trabajo, y disipar calor.

El movimiento en el tiempo de 25 partículas en un recipiente cerrado y sin fronteras, se puede aproximar mediante una simulación por ordenador con mucho detalle utilizando el potencial de Lennard-Jones. Vamos a observar el movimiento natural de un sistema de este tipo en el siguiente vídeo. Como se puede ver, los estados que aparecen son poco complejos y pertenecen al grueso del numeroso subconjunto de estados posibles desordenados. Para ver algún tipo de complejidad aparecer espontáneamente en este sistema, tendríamos que esperar probablemente muchos años:

Si embargo, si forzamos a este sistema a adquirir estructuras complejas mediante un algoritmo (cosa que no se puede hacer en un laboratorio real), podemos corroborar que se cumple el postulado de partida de toda la teoría de Jeremy England: a más complejidad estructural, más energía se requiere consumir. Si el consumo baja, la complejidad baja; y si el consumo se mantiene la complejidad se mantiene.

En el siguiente vídeo, se puede observar un ejemplo que muestra como, una vez hemos forzado al sistema inicial caótico hacia la complejidad, siempre se acaba con menos energía de la cantidad media que suele haber en sistemas poco complejos. Nunca se llegan a observar sistemas poco complejos que sean grandes disipadores de calor, ni tampoco se observan sistemas complejos que disipen poco calor. ¡Ambas cualidades están correlacionas por la física subyacente al mundo!

Este vídeo muestra cómo el sistema, una vez lo forzamos a la complejidad, se ha adaptado de un modo automático, natural y espontáneo hacia un estado el cual posee la cualidad de disipar mucho más calor que la media. Y no es que nosotros le indiquemos al sistema como debe moverse, sino que simplemente señalamos que tipo de complejidad buscamos, y el sistema automáticamente se adapta hacia dicha complejidad utilizando el camino más probable, que vemos que se corresponde siempre (y esto lo comprobamos a posteriori) con las trayectorias que más energía consumen: y esto es precisamente lo que la teoría señala desde las matemáticas. Es muy interesante ver como aparecen diversas agrupaciones y patrones orbitales en esta simulación, cuando en ningún momento se programa este comportamiento, el cual surge espontáneamente (observar la diferencia entre estos patrones que digo, y el comportamiento natural de este tipo de sistemas que vimos en el primero vídeo).

En una próxima entrada, mostraré un nuevo experimento en el que pretendo mostrar, con una simulación más elaborada, este mismo resultado pero de un modo más claro si cabe.

Estad atentos ;).

Evidencia a favor de la teoría de Jeremy England

"You start with a random clump of atoms, and if you shine light on it for long enough, it should not be so surprising that you get a plant."

Jeremy England (2014), interview commentary with Natalie Wolchover

Hace ya un mes que terminé de estudiar a fondo el interesante trabajo que el físico Jeremy England está realizando en el MIT (Massachusetts Institute of Technology). En mi blog he divulgado todo lo referente a este trabajo con mucho nivel de detalle, siendo esta entrada un compendio de todo lo que el trabajo cuenta.

La idea de esta línea de investigación viene a decir, a grosso modo, que la física de nuestro mundo mantiene una relación implícita entre complejidad y energía. Esta relación indica que, cuanto más complejo es un fenómeno, más energía debe disiparse de modo que crezca la probabilidad de que tal fenómeno finalmente acontezca. Esta teoría de Jeremy parte, y se deduce, de una base termodinámica y de mecánica estadística ya establecida, por lo que sus conclusiones teóricas se toman ya por ciertas. El equipo simplemente necesita un mayor apoyo experimental que respalde su propuesta, y yo creo haber conseguido aportar un granito de arena en este sentido, luego veremos cómo.

Desde el primer momento, la idea de esta investigación me atrajo sobremanera. Realmente es cierto que cualquier fenómeno complejo que observamos (y no sólo en el terreno biológico) es un gran devorador relativo de energía. Además, podemos ver que cuanto más complejo es un fenómeno, más energía parece necesitar para su formación y mantenimiento; siendo, por cierto, el fenómeno que más energía consume aquí en la Tierra, también el más complejo que observamos: el sistema social humano.

La teoría de Jeremy técnicamente se resume en la siguiente fórmula:

Es cierto que esta fórmula intimida en un primer vistazo, pero es sólo porque normalmente no se conoce el significado de gran parte de los símbolos que se utiliza. Podéis ver el desarrollo completo que lleva a esta fórmula desde esta entrada de mi blog. En realidad, con las matemáticas del bachillerato (y quizás un poquito más) es suficiente para seguir el proceso.

Esta fórmula presupone su validez en un sistema físico muy determinado. Es decir; que para que se cumpla, debemos estar estudiando un sistema que cumpla lo siguiente:

Ser,

 1) Un sistema lejos del equilibrio térmico (como por ejemplo, la Tierra).
2) Poseer una fuente constante de energía externa entrando en dicho sistema (como es el caso del Sol).
3) Y que posea también un gran baño térmico donde disipar calor (como es el caso de la atmósfera o el océano en la Tierra).

Todo sistema que cumpla estas tres condiciones, en teoría debería evolucionar siguiendo la fórmula que acabamos de ver. Y la fórmula, a grosso modo, nos indica la probabilidad de observar determinados fenómenos macroscópicos según sean sus propiedades físicas:

Los dos primeros términos de la fórmula, nos dicen que el sistema tiende espontáneamente hacia fenómenos macroscópicos caóticos y sin orden; sistemas que son fácilmente reversibles en el tiempo. Y esto es así por la sencilla razón de que hay más sistemas de este tipo: si dividimos el conjunto de estados posibles entre estados desordenados y caóticos, y estados ordenados que siguen un patrón; se puede comprobar que el primer subconjunto (el subconjunto que engloba los estados desordenados) contiene un número astronómicamente mayor de elementos que el subconjunto de estados ordenados y complejos.

Y este dominio de estados desordenados posibles sobre estados ordenados posibles, es el que hace que la probabilidad de observar sistemas desordenados sea muchísimo mayor cuando se deja evolucionar libremente sistemas físicos en el mundo. Esto lo expresa matemáticamente la fórmula anterior con sus dos primeros términos. El primero lo hace de un modo explícito, y el segundo término es consecuencia del primero: un sistema reversible es más probable de observar, puesto que es más fácil de alcanzar. Y es que, si un sistema es poco reversible, es porque para ser alcanzado dicho sistema debe haber seguido un patrón complejo (pasando por sucesivos estados del subconjunto mucho menos numeroso de estados posibles ordenados).

El tercer y cuarto término de la ecuación, nos indican algo muy interesante: la probabilidad de alcanzar fenómenos complejos y ordenados (que hemos visto que pertenecen al subconjunto de estados físicos posibles astronómicamente menos numeroso) puede aumentar, con tal de que la suma de estos dos términos aumenten en proporción a la complejidad que se quiere observar.

Es decir; que aunque el subconjunto de estados ordenados sea enormemente reducido, es posible favorecer la probabilidad en la aparición de dichos fenómenos complejos, a condición de que dicho fenómeno complejo consiga, o mejor dicho, que posea la propiedad de ser eficiente aumentando el calor medio disipado en su formación y mantenimiento (el tercer y cuarto miembro de la ecuación reflejan precisamente esto: el calor disipado de media) .

Por lo tanto: la probabilidad de observar fenómenos complejos espontáneamente en estos sistemas lejos del equilibrio térmico es prácticamente imposible (ya que, como hemos dicho, el subconjunto de estados ordenados posibles es inmensamente menor en tamaño al de estados desordenados posibles) a menos de que el tercer y cuarto término (el calor medio disipado) sea lo suficientemente alto como para compensar el bajo valor de los dos primero térmicos (bajo valor que hemos visto es consecuencia de la supremacía de estados desordenados hacia los que puede ir el sistema).

Bien. Esto es la teoría, y además es una teoría contrastable. De hecho, los chicos del  MIT ya han encontrado respaldo en ciertos experimentos realizados, aunque aún nada determinante. Yo, por mi parte, creo haber encontrado un modo de apoyar la teoría de Jeremy England haciendo uso de lo que es mi área de estudio: la computación.

Objetivo del trabajo.

Es muy complejo respaldar directamente en un laboratorio esta teoría, puesto que para estudiar la posible relación entre complejidad y calor disipado, en principio habría que estudiar un sistema lejos del equilibrio térmico, y comprobar la relación entre la complejidad de lo observado con el calor que disipó su formación. El problema principal que yo veo, es que si se quiere estudiar sistemas complejos reales que surjan espontáneamente en un laboratorio, y si la relación entre complejidad y baja probabilidad de ocurrencia es cierta, habría que esperar cientos de miles de horas (o años) para que finalmente ocurra dicho fenómeno (y calcular el calor disipado). Es decir; y para poner un ejemplo extremo que clarifique el problema: si ponemos en una maceta todos los componentes individuales necesarios para formar una planta y lo dejamos reposar al Sol, necesitaríamos de millones de años para que la compleja planta se formara al azar y medir así el calor disipado: no es práctico (xDD). Se podría, evidentemente, intentar estudiar de este modo fenómenos menos complejos (y por lo tanto más probables) que una planta, pero el problema es que cuanto menos complejo sea el fenómeno, menos evidente va a ser la correlación entre calor y complejidad (ya que ésta va a ser menor), y cualquier correlación observada (al ser débil) se podría achacar a otros factores ambientales o a errores de medición.

En realidad hay otros métodos menos directos de contrastar esta teoría, y me consta que el equipo de Jeremy está en ello, pero desde el principio se me ocurrió un modo de poder estudiar el asunto desde esta perspectiva más directa de la que hablo: utilizando la simulación por ordenador.

¿En qué consiste mi prueba experimental?

La idea es la siguiente:

1) Programamos un sistema físico que simule lo mejor posible la realidad física.
2) Programamos un modo de calcular la energía del sistema conforme el sistema evoluciona en el tiempo.
3) Procedemos a buscar sistemas complejos mediante computación evolutiva.
4) Calculamos el calor disipado en la formación de tales sistemas ordenados.
5) Estudiamos si existe correlación en esta simulación, entre la complejidad alcanzada y el calor disipado.

Y para reforzar aún más el estudio experimental, procedemos de nuevo, pero sustituyendo el paso 3) y 4) por lo siguiente:

3) Procedemos a buscar sistemas que disipen poco calor mediante computación evolutiva.
4) Calculamos la complejidad del sistema cuando se disipa poco calor.

Si la correlación propuesta entre complejidad y calor disipado es correcta, los sistemas complejos deberán de ir siempre (en la práctica) acompañados de una gran cantidad de calor disipado (energía útil consumida).

¡Y es precisamente esto lo que he observado cuando he realizado este experimento!

¿Cómo he procedido a realizar la prueba?

Para el punto 1) y 2) me ayudé de una librería de Java llamada Opensourcephysics. Esta librería (de código abierto) ha sido realizada precisamente para ayudar en la simulación de sistemas físicos.

En concreto, partí de la simulación que incluye el paquete (en org.opensourcephysics.sip.ch08.md) de sistemas de potencial de Lennard-Jones. El potencial Lennard-Jones es usado muy comúnmente en la simulación por ordenador debido a que es una buena aproximación a la física de partículas real, y a que, aún siendo un modelo simple, permite un detallado estudio de las propiedades de los gases y de las interacciones en modelos moleculares.

Esta librería de Java ya incluía pues lo que necesitaba para comenzar a experimentar: una simulación física bastante aproximada, pero a la vez lo más sencilla posible. Por cierto que la simulación del potencial L-J que incluye Opensourcephysics fue desarrollado originalmente en el 2006 por Jan Tobochnik, Wolfgang Christian, y Harvey Gould.

Así que sobre la simulación de estos sistemas comencé a trabajar y a programar el resto de la prueba.

Lo primero que hice fue implementar uno de los requisitos que la teoría requiere: que el sistema sea expuesto a una fuente de energía externa constante. ¿Cómo lo hice? Pues simplemente simulando que el sistema L-J está bajo una lluvia constante de partículas externas que eventualmente pueden chocar con las partículas del sistema haciéndoles cambiar el sentido de su movimiento en las coordenadas x e y. Esta lluvia de partículas virtuales añadidas (emulando a la lluvia de fotones que llegan desde el Sol a la Tierra) tras ocasionalmente golpear e interactuar con las partículas de nuestro sistema, simplemente desaparecen.

Ahora ya tenía lista una simulación bastante aproximada a la realidad física, y que cumplía las tres condiciones previas de la propuesta teórica de Jeremy England.

Paso 3): ¿Por qué introducir un algoritmo de computación evolutiva?

Si me hubiese limitado a observar como evoluciona espontámente este sistema L-J modificado, me habría encontrado en la misma situación, y con el mismo problema, que en el laboratorio: tener que esperar una enorme cantidad de tiempo hasta que diese la causalidad de que un fenómeno complejo aconteciera en la simulación física para poder calcular así el calor disipado.

En el mundo real no podemos acelerar artificialmente la ocurrencia de tal complejidad, por ejemplo en una matraz o en una placa de Petri, pero; y aquí viene la clave del asunto, en nuestra simulación sí que podemos buscar o dirigir el sistema hacia la complejidad de un modo intencionado, acortando enormemente el tiempo de espera necesario para que surjan patrones complejos y ordenados. ¿Y de qué modo es posible tal búsqueda capaz de lograr alcanzar la complejidad en un corto espacio de tiempo (en comparación con el tiempo necesario para que ocurra por azar)? Pues sí, como no: mediante un proceso evolutivo. En concreto, hice uso de las propuestas de la computación evolutiva (puedes ver algunas entradas donde trato sobre algoritmos evolutivos aquí).

Esa fue la razón de añadir el tercer paso comentado: lograr, mediante un proceso evolutivo computacional, observar patrones y sistemas complejos en nuestra simulación sin tener que esperar todo el tiempo que sería necesario para que la complejidad ocurriera de forma espontánea. Además, actuando de este modo, vamos a poder dirigir el sistema hacia sistemas con las propiedades deseadas en cada caso; lo que nos permitirá estudiar más fácilmente si existe o no correlación entre orden y consumo de energía.

Medición de la complejidad.

En este punto se presenta un problema: ¿cómo medir o calcular la complejidad de un sistema determinado? Para solucionar este problema, simplemente hice uso del sentido común. La presencia de patrones, agrupaciones, y orden de cualquier tipo es signo evidente de complejidad (ya que dichos estados son pocos numerosos de entre todas las posibilidades físicas); por lo que, un modo sencillo de medir la complejidad, consiste en simplemente estudiar la cercanía entre cada par de partículas. Cuanto más cercanas estuvieran las partículas entre sí; menos reversible será el sistema en el tiempo respecto al estado de partida (segundo término con un bajo valor), y, además, existirán muchas menos configuraciones posibles con todas las partículas cercanas, que configuraciones con las partículas distribuidas al azar (lo que implica un bajo valor para el primer término).

Hay que aclarar aquí, que aunque se utilice un proceso evolutivo para lograr alcanzar estados complejos en cortos periodos de tiempo; eso no implica que se alcanzará cualquier tipo de sistema, sino que el algoritmo evolutivo va a encontrar aquellos estados más probables o fáciles de alcanzar. Y resulta que, según la teoría de Jeremy, los sistemas más probables (cuando los dos primeros términos tienen bajo valor) son aquellos sistemas que disipan gran cantidad de calor en el proceso. Por lo tanto, una vez finalizado el proceso evolutivo (tras pasar las n generaciones programadas), se habrán seleccionado aquellos estados más complejos pero también aquellos más accesibles (y fáciles de alcanzar), los cuales; según la teoría, deberán ser aquellos que mejor se adapten a la fuente de energía externa para realizar trabajo (y consumir energía útil disipando gran cantidad de calor).

Resultados del estudio I.

En el primer caso de estudio, vamos en 3) a dirigir el sistema evolutivamente hacia sistemas complejos (con todas sus partículas lo más cercanas posibles unas de otras), y procederemos a estudiar el calor disipado en el proceso:

En este estudio vamos a trabajar con N = 25 partículas, moviéndose en una superficie (bidimensional) de  longitud Lx = 25 y Ly = 20. Esta superficie no tiene fronteras, lo que significa que, por ejemplo; la partícula que salga por la derecha, entrará por la izquierda a la misma altura (la Tierra es un sistema sin fronteras de este estilo, sólo que tridimensional y en forma de esfera). Se ajusta, además, una energía cinética inicial por partícula igual a la unidad.

El algoritmo evolutivo procederá utilizando una población constante de i = 250 sistemas L-J (individuos), y durante g = 1250 generaciones antes de parar (condición de parada t > g). Cada 100 pasos (1 segundo aproximadamente), se evaluará la complejidad de cada individuo (como de cerca están sus partículas), y se seleccionarán aquellos individuos más adaptados (es decir, aquellos más complejos). De cada superviviente se creará un clon, y se aplicará una mutación, la cual consiste simplemente en aplicar el campo de fuerza externo del que hablamos antes (la lluvia de fotones virtuales que pueden eventualmente cambiar la dirección y sentido de algunas partículas del sistema).

Los sistemas que presenten la propiedad de ser los que mejor se adaptan a esta lluvia de fotones virtuales de modo que permitan la aparición de la complejidad buscada, serán los que vayan sobreviviendo al proceso. De este modo, se consigue que al finalizar la búsqueda evolutiva, obtengamos una población de sistemas L-J, cuyas trayectorias han ido siguiendo caminos poco reversibles y complejos, y al mismo tiempo adaptados a la fuente de energía externa.

Según la teoría, todos estos sistemas complejos finales deben haber disipado una enorme cantidad de calor para ser alcanzados (recordemos que el algoritmo evolutivo va a encontrar los sistemas complejos más probables), lo que se traduce en que la energía útil final de los individuos complejos debe ser mucho menor que la energía útil que tendría el mismo sistema original si no se hubiese guiado hacia la complejidad.

Veamos que ocurre al poner en práctica este experimento:

Para aclarar los resultados, hay que tener en cuenta que todo el proceso evolutivo comienza con i = 250 clones perfectos de un sistema aleatorio original al que denominamos Sistema Lennard-Jones I (o mdI para abreviar). Este sistema L-J de inicio (mdI) lo haremos evolucionar junto a la población pero sin ser guiado evolutivamente: es decir; que se le permitirá moverse durante los mismos pasos que a los individuos evolucionados, para que nos sirva así de sistema de control con el que comparar respecto al calor que disipa un sistema poco complejo de un modo natural.

Al finalizar el proceso evolutivo, vamos a seleccionar el mejor individuo de la población final de 250 supervivientes de sistemas L-J (es decir, el más complejo). A este individuo seleccionado lo llamaremos Sistema Lennard-Jones II (o mdII para abreviar).

Una vez tenemos a mdI y a mdII, tendremos ya dos sistemas que habrán recorrido el mismo número de pasos, pero que han seguido trayectorias diferentes en cuanto a complejidad. mdI habrá seguido trayectorias probables y espontáneas dominadas por los dos primeros términos de la ecuación de Jeremy, mientras que mdII habrá seguido caminos cada vez más complejos e irreversibles. Si la teoría del equipo del MIT es cierta, mdII debe haber disipado mucho más calor que mdI en el mismo número de pasos (el mismo intervalo de tiempo acontecido). Además, deberá existir una correlación directa entre complejidad y calor disipado, de modo que cuanto mayor complejidad conseguida por el proceso evolutivo, menos energía final tendrá el sistema (más calor disipó en su trayectoria).

Veamos los resultados:

Antes de nada, os muestro un vídeo animado de lo que es la evolución temporal natural de un sistema  L-J como el que estamos estudiando. Como se puede observar, los estados que aparecen son poco complejos y pertenecen al grueso del numeroso subconjunto de estados posibles desordenados. Para ver algún tipo de complejidad aparecer espontáneamente en este sistema, tendríamos que esperar probablemente muchos años:

Sistema Lennard-Jones I (mdI) sin dirigir

A continuación, podéis ver una imagen con el estado inicial mdI, y el mismo estado inicial una vez que éste ha sido dirigido hacia un estado complejo (mdII):

 

Sistema Lennard-Jones I (mdI) tras
 125000 pasos (125 segundos aprox.)

Sistema dirigido Lennard-Jones II (mdII) tras 
los mismos 125000 pasos 
(125 segundos aprox.)

Como se puede observar, hemos conseguido que el sistema L-J alcance una complejidad que podríamos estar años esperando que ocurriera de forma natural. Y, lo que es más importante ¡la complejidad alcanzada es poco reversible tal y como Jeremy England afirma en sus estudios!  Según la teoría, una vez se alcanza tras un periodo de tiempo una gran complejidad gracias a una alta disipación de calor, es muy poco probable que el proceso inverso ocurra en el mismo intervalo de tiempo. Os muestro a continuación un vídeo donde podréis observar como el estado mdII, una vez el algoritmo evolutivo deja de actuar, no vuelve rápidamente a un estado más desordenado, sino que permanece mostrando el patrón ordenado que ya alcanzó:

Paso 5) Estudio de la correlación entre calor disipado y nivel de complejidad alcanzado.

Como ya se ha comentado, la complejidad se mide según sea la distancia entre cada par de partículas. Para que el proceso evolutivo pueda distinguir entre los mejores individuos de la población de sistemas L-J, se va estudiando la complejidad media alcanzada en un número de pasos dados:

Complejidad media alcanzada = complejidad / número de pasos

donde la complejidad es simplemente la suma de la distancia de cada par de partículas.

Los valores de esta Complejidad media alcanzada van a ir tendiendo a cero conforme la complejidad aumenta en el tiempo, puesto que el número de pasos (denominador) va aumentando mientras que la suma de complejidad (numerador) llega un momento que apenas aumenta. Los valores de la complejidad media serán tanto mejores cuanto más cerca del cero se encuentre. Una complejidad media de 0,5 viene a representar un estado que ha evolucionado de un modo totalmente caótico con las partículas esparcidas de un modo más o menos homogéneo por toda la superficie.

Para más claridad, y antes de mostrar la tabla de resultados, voy a mostrar la apariencia final según la complejidad alcanzada en el proceso dirigido en varios sistemas L-J:

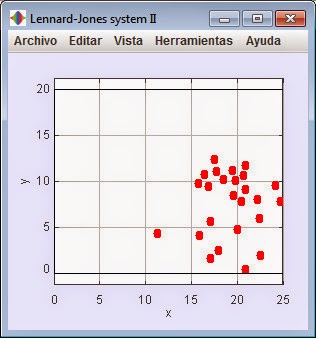Apariencia de sistema L-J (mdII) con una complejidad
 media conseguida de 0.20

Evolución posterior de este sistema L-J (mdII) con una 

complejidad media conseguida del 0.20

Apariencia de sistema L-J (mdII) con una complejidad
 media conseguida de 0.04

Apariencia de sistema L-J (mdII) con una complejidad
 media conseguida de 0.065

Apariencia de sistema L-J (mdII) con una complejidad
 media conseguida de 0.060

Evolución posterior de un sistema L-J (mdII) con una complejidad
 media conseguida de 0.060

Medición del calor disipado.

El calor disipado lo vamos a medir simplemente tomando la energía inicial (suma de energía cinética y potencial) y restando la energía final. Esta diferencia en la energía va a representar el calor que se disipado en el proceso. Calor disipado que, según la teoría, debe ser tanto mayor, cuanto mayor complejidad se alcance.

Mostramos a continuación la tabla de resultados del calor disipado (tras 125000 pasos) según el nivel de complejidad medio alcanzado, y comparado en relación a un sistema de control. El sistema L-J de control, como hemos visto, no es más que el mismo sistema inicial mdI pero que procede el mismo número de pasos que mdII aunque sin ser dirigido:

Complejidad mdII:      Energía final mdI:     Energía final mdII:     Calor disipado (mdI - mdII):

0.410                    2665936.29              2651880.45                           14055.84
0.195                    2633071.24                951213.39                       1681857.84
0.064                    2680313.52                634706.74                       2045606.77
0.060                    2687338.15             -1169582.75                       3856920.91
0.051                    2697423.30               -506615.05                       3204038.36


¡¡Se puede ver una indudable correlación entre la complejidad media del sistema y calor disipado en el proceso!!

Pero para reforzar más estos datos, vamos a proceder a continuación a mostrar un seguimiento de la evolución en las 1250 generaciones del mejor individuo, realizando una comparación como la anterior donde veremos la relación entre el calor disipado en cada generación con la complejidad alcanzada hasta ese momento. La correlación entre complejidad y cantidad de calor disipado es innegable:

Generación   Complejidad mdII:      Energía mdI:     Energía mdII:     Calor disipado (mdI - mdII):

125                   2.578                            291576.44            162282.31             129294.12
250                   1.194                            558308.67            221265.40             337043.27
375                   0.475                            829178.78            203825.56             625353.22
500                   0.301                          1075901.39              22840.16           1053061.22
625                   0.141                          1339369.76           -210296.34           1549666.10
750                   0.145                          1605291.85           -445750.92           2051042.77
875                   0.112                          1866449.60           -669400.96           2535850.56
1000                 0.151                          2142136.75           -885776.27           3027913.02
1125                 0.108                          2415270.38         -1108760.68           3524031.06
1250                 0.055                          2679966.69         -1350419.40           4030386.10

La correlación es más que evidente comparando los valores de la columna de complejidad mdII con la columna del calor disipado. A mayor complejidad (cuanto más cerca de 0 está el valor) mayor calor disipado con respecto al sistema de control mdI  (que mantiene su complejidad muy baja en el tiempo).

Sistema inicial mdI de la tabla anterior

Sistema mdII de la tabla anterior tras las 1250 generaciones

Complejidad irreversible.

Si, una vez alcanzado un estado complejo, dejamos a continuación evolucionar el sistema libremente; tal y como afirma la teoría, no se vuelve instantáneamente al desorden, sino que el orden conseguido se mantiene conforme pasa el tiempo. Al haberse liberado mucho calor y haberse consumido mucha energía útil, las matemáticas del estudio nos cuentan que el proceso alcanzado va a ser bastante irreversible en el mismo periodo de tiempo invertido ¡y eso es lo que se observa! Os dejo a continuación un vídeo donde se observa la evolución de un sistema mdII de alto nivel de complejidad alcanzado. Podéis ver como aún pasando mucho tiempo, la agrupación de las partículas se mantiene, formándose diversos tipos de patrones y agrupaciones (e incluso órbitas):

 

Es más, conforme el sistema complejo sigue evolucionando libremente, ¡se puede comprobar como sigue disipando mucha más energía que el sistema caótico de control! Cosa que sigue estando de acuerdo con la teoría de Jeremy England, puesto que la complejidad, para permanecer en el tiempo, requiere de una constante disipación de calor que contrarreste la irreversibilidad y la baja probabilidad de su complejidad.

Anotaciones sobre el estudio:

No nos llevemos a engaño. El uso de un algoritmo de computación evolutiva no interfiere directamente en el modo en que el sistema cambia en el tiempo, sino que simplemente es una herramienta que nos ayuda a buscar de entre todas las posibles trayectorias naturales, aquellas que conducen a patrones complejos sin la necesidad de tener que esperar años a que esto ocurra de un modo natural. Es sólo un modo de disminuir exponencialmente el tiempo requerido para poder estudiar sistemas complejos que son poco probables de acontecer espontáneamente, pero lo hace sin interferir directamente en el desarrollo del sistema físico: se trata sólo de ver y seleccionar lo que nos interesa, desechando las alternativas que son poco prometedoras como candidatas a finalizar en sistemas complejos.

Es decir; que es muy importante comprender que, pese al uso del algoritmo evolutivo, los datos obtenidos, y que se han mostrado en las tablas anteriores, son exactamente los mismos que obtendríamos si esperásemos durante años hasta que un estado complejo del estilo que hemos estudiado apareciera de un modo natural y espontáneo.

Resultados del estudio II.

En este segundo caso de estudio, vamos en el paso 3) a dirigir el sistema evolutivamente, no hacia sistemas complejos somo hicimos antes, sino hacia sistemas que disipen poca cantidad de calor. Si la teoría que pretendemos corroborar es cierta, también debería observarse una correlación entre un menor consumo de energía y una menor complejidad:

Vamos a trabajar aquí también con N = 25 partículas, moviéndose en una superficie (bidimensional) de  longitud Lx = 25 y Ly = 20.

Para realizar este estudio, vamos a partir de un sistema L-J muy complejo (mdII), y a observar qué ocurre si dirigimos este sistema hacia bajos niveles de calor disipado (valores bajos del tercer y cuarto término). La teoría afirma que, puesto que comenzamos en un estado muy ordenado (primer y segundo término bajo), la probabilidad de observar tal complejidad con cierta frecuencia ha sido respaldada por una alta disipación de energía previa. Si ahora buscamos sistemas que partan de este sistema complejo (mdII) pero que cada vez disipen menos calor, debe ocurrir la correlación inversa a la del estudio I: cuanto menos calor disipe el camino o trayectoria, más complejidad debe haber perdido (más debe haber subido el primer y segundo término para respaldar la bajada en los términos tercero y cuarto).

Así, si partimos de un sistema complejo y este sistema empieza a disipar menos calor, debe ser a costa de disminuir su complejidad.

Técnicamente, este estudio lo he realizado del siguiente modo:

1) Procedemos como en el estudio I buscando sistemas complejos en 1250 generaciones (125000 pasos) a partir de un sistema origen mdI.
2) Seleccionamos el mejor individuo de la población final (mdII) y medimos el calor disipado y la complejidad alcanzada.
3) Procedemos a buscar evolutivamente sistemas con bajo calor disipado a partir del anterior mejor individuo mdII. Tras otras 1250 generaciones (otros 125000 pasos), seleccionamos al mejor individuo de la población final (mdI*).
4) Medimos la complejidad de mdI* y el calor disipado, y comparamos con el sistema de control (mdII) el cual habrá dado también 125000 pasos pero sin ser dirigido a menores niveles disipativos.

Si la teoría es correcta, el sistema mdI* deberá poseer unas características muy similares al mdI original en cuanto a complejidad se refiere.

Mostramos a continuación los resultados de este estudio:

Complej. mdI:   0.345  Energía mdI:     2663414,03

Complej.mdII:  0.063  Energía mdII:     -535605,01  Disipado (mdI - mdII):     3199019,04

Complej.mdI*:  0.401  Energía mdI*:    3135984,42 Disipado (mdII - mdI*):  -3671589.43 (el sistema no consume y disipa energía útil, sino que la adquiere)

Se puede observar como una disminución en el calor disipado (la energía útil consumida) va acompañada de un descenso en la complejidad, como se pretendía comprobar.

En las siguientes instantáneas se puede observar como evoluciona el sistema cuando primero alcanza gran complejidad mediante el uso de mucha energía, y de como el sistema vuelve a perder complejidad estructural en cuanto el calor disipado disminuye en el tiempo:

Sistema aleatorio original mdI

Sistema final mdII tras las primeras 1250 generaciones
buscando alta complejidad. Este sistema es el que
usamos para buscar a partir de él alta disipación

El mismo sistema mdII tras haber servido de control
moviéndose libremente 125000 nuevos pasos

Sistema final mdI* tras buscarse durante 1250
generaciones a partir de mdII sistemas que
disipen poca cantidad de calor. Se puede observar
como la complejidad se pierde

Y para terminar, sólo señalar que, si repetimos este último experimento pero procedemos a partir de mdII a buscar evolucitvamente sistemas que disipen más calor (en lugar de menos como antes), también vemos como el sistema se ajusta a lo que la teoría predice: el sistema final mdI* tras las 2500 nuevas generaciones va a ser de una complejidad similar a mdII:

Complej. mdI:   0.412  Energía mdI:     2637496.65

Complej.mdII:  0.058  Energía mdII:     -458086.05  Disipado (mdI - mdII):   3095582.70

Complej.mdI*:  0.046  Energía mdI*:  -3359158.03 Disipado (mdII - mdI*):  2901071.98

Sistema aleatorio original mdI

Sistema final mdII tras las primeras 1250 generaciones
buscando alta complejidad. Este sistema es el que
usamos para buscar a partir de él alta disipación.

El mismo sistema mdII tras haber servido de control
moviéndose libremente 125000 nuevos pasos

Sistema final mdI* tras buscarse durante 1250
generaciones a partir de mdII sistemas que
disipen alta cantidad de calor. Se puede observar
como la complejidad se mantiene e incluso 
aumenta en este caso

Vídeo que muestra el movimiento libre de un sistema mdI* tras haber sido

evolucionado buscando complejidad 1250 generaciones a partir de mdI,

y haber sido más tarde evolucionado buscando alta disipación de calor otras

 1250 generaciones a partir de mdII

Este último ejemplo demuestra como, una vez un sistema complejo ha sido alcanzado, el mantenimiento o el aumento en el calor disipado sólo es posible si se mantiene la complejidad; siendo muy poco probable que la complejidad caiga y aún así se disipe más. El ejemplo anterior nos mostró el caso opuesto, como una vez alcanzada la complejidad se requiere mantener el nivel de calor disipado para mantener la complejidad, siendo muy poco probable que la complejidad se mantenga y el calor disipado descienda.

Conclusión.

Mediante este doble estudio experimental se ha podido corroborar en sistemas físicos simulados mediante sistemas de potencial de Lennard-Jones la propuesta teórica de Jeremy England. Ciertamente hemos observado una correlación muy clara entre calor disipado (energía consumida por un trabajo) y complejidad estructural. Además, dicha correlación se da tanto si se buscan sistemas complejos (en cuyo caso se observa que el calor disipado es mucho mayor del normal), como si se buscan sistemas que disipen poco calor (en cuyo caso se observa una disminución en la complejidad estructural y un aumento del desorden).

Todo esto parece apoyar sin duda la teoría matemática que precisamente se fundamenta en lo que acabamos de decir: que los fenómenos físicos complejos sólo son asequibles estadísticamente si sus propiedades los hacen buenos disipando gran cantidad de calor (ya que eso aumenta su probabilidad de ocurrencia). En otras palabras: un sistema complejo cuyas propiedades no lo hagan eficientes consumidores de energía, es casi imposible que acontezca de un modo espontáneo; pero sin embargo, si las propiedades de este sistema lo hacen eficientes consumidores de energía, la física del mundo hará que la probabilidad de ocurrencia de tal complejidad sea mayor que en el caso contrario.

Esto no implica en absoluto que la complejidad surja por doquier sino que nos aclara que, cuando surge, es porque la probabilidad de tal complejidad ha aumentado lo suficiente (dada la oportunidad) gracias al tercer y cuarto término del que hemos hablado. Por lo tanto, conforme el tercer y el cuarto término van creciendo (calor medio disipado), nos podemos permitir que el primero y el segundo término vayan bajando (aumentando el nivel de complejidad). Se produce así una especie de adaptación gradual hacia la complejidad a costa de consumir cada vez más trabajo. Esta es precisamente la tesis de Jeremy, y es lo que hemos observamos en nuestros estudios de simulación.

En resumen: que es simplemente este proceso gradual adaptativo (físico y espontáneo) en favor de la eficiencia en la generación de calor, el que permite observar fenómenos cada vez más organizados y complejos en sistemas lejos del equilibrio térmico. Este proceso de adaptación natural es, en palabras de Jeremy, el culpable de cualquier tipo de proceso evolutivo en el Universo, y este proceso de adaptación natural, es también el que originalmente permitió la organización de ciertas moléculas en nuestro planeta, y el que terminó al cabo de millones de años dando lugar a la vida en la Tierra.

Además, esta tendencia física que correlaciona complejidad y consumo energético, debe obligatoriamente cumplirse en cualquier fenómeno macroscópico complejo del mundo, puesto que todo fenómeno se basa en una física subyacente. Por lo tanto, se puede concluir que todo fenómeno complejo existe gracias a (y se fundamente en) consumir y devorar energía. Y esto incluye, por supuesto, al hombre y a toda su conducta.

Se puede leer un resumen mucho más amplio y explicativo de esto último que he comentado en esta otra entrada de mi blog.

Código fuente de los experimentos.

Si alguien está interesado en estudiar más a fondo los ejemplos propuestos, me podéis pedir en un comentario en esta misma entrada el código fuente del programa que he desarrollado para realizar las pruebas que he descrito.

Simplemente es requisito que sepáis programar en Java, que instaléis el Eclipse en vuestro ordenador, y que importéis la librería Opensourcephysics. Finalmente sólo deberéis importar en el workspace los ficheros java que yo os pasaré por correo, y ya podréis hacer todas las pruebas que queráis modificando los parámetros de configuración ;).

Aquí tenéis todas las referencias necesarias para seguir este interesante asunto:

1. http://www.englandlab.com/publications.html (web oficial del equipo de investigación de Jeremy England. Aquí irán subiendo los avances que se produzcan en este asunto).
2. G. E. Crooks, Phys. Rev. E 60, 2721 (1999). [3] R. A. Blythe, Phys. Rev. Lett. 100, 010601 (2008). (Este estudio de Crooks, es el que sirve de base para todo el trabajo de Jeremy).
3. Perunov, N., Marsland, R., and England, J. "Statistical Physics of Adaptation", (preprint), arxiv.org, 2014. (Este es el paper de diciembre que ha levantado tanta expectación).
4. England, J. L.  "Statistical Physics of self-replication." J. Chem. Phys., 139, 121923 (2013). (Este es un paper del 2013, donde el equipo comenzó a dar forma definida a toda la línea de investigación).
5. https://www.youtube.com/watch?v=e91D5UAz-f4#t=1720 (Vídeo con una charla del propio Jeremy England donde explica la línea de investigación).
6. http://www.scientificamerican.com/article/a-new-physics-theory-of-life/ (Artículo divulgativo en la revista Scientific American sobre el trabajo de Jeremy England).
7. https://www.quantamagazine.org/20140122-a-new-physics-theory-of-life/ (Artículo divulgativo en la revista Quanta Magazine sobre el trabajo de Jeremy).
8. Artículo donde explico en detalle qué es un algoritmo evolutivo: http://quevidaesta2010.blogspot.com.es/2011/08/computacion-evolutiva-ejemplo-i.html
9. Artículo divulgativo, donde explico en más profundidad las implicaciones del trabajo teórico de Jeremy England: http://quevidaesta2010.blogspot.com.es/2015/02/las-matematicas-de-la-conducta.html
10. http://quevidaesta2010.blogspot.com.es/2014/12/las-matematicas-de-la-vida.html
11. http://quevidaesta2010.blogspot.com.es/2015/01/las-matematicas-de-la-vida-ii.html
12. http://quevidaesta2010.blogspot.com.es/2015/01/las-matematicas-de-la-vida-iii.html
13. http://quevidaesta2010.blogspot.com.es/2015/01/las-matematicas-de-la-vida-iv.html
14. http://quevidaesta2010.blogspot.com.es/2015/01/las-matematicas-de-la-vida-v.html
15. Librería de código abierto para la simulación de sistemas físicos: Opensourcephysics
16. Enlace externo donde se explica en qué consiste y qué es el potencial de Lennard-Jones.