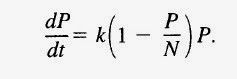La vida, la vida, la vida es, es un contratiempo, la vida, la vida es...

Sobran las palabras. Sentimiento en estado puro:

El Niño Perdido - La Cigarra (Camarón De La Isla)

Que mala suerte la mía, 
de haber tropezao contigo, 
lo a gustito que yo vivía, 
tu cariño es mi castigo. 

Me voy de estos terrenos 
que ya he renunciaíto primita mía 
pa toíta la vía, 
sólo por no escuchar tú nombre, 
que yo me voy a la morería. 

Ay, luna que brilla en los mares, 
en los mares oscuros, 
luna, tú no estás cansá 
de girar el mismo mundo, 
ay, luna quédate conmigo, 
ya no te vayas, 
porque dicen que a veces 
se tarda el alba. 

Camino de Pozo Blanco 
había una tabernita 
con vino blanco. 
Échame otro buchito, 
vengo najando, 
no ha catao ná. 

Después me nació un clavel 
pa alegrarme a mí los días, 
y ahora que tengo a los tres, 
que maravilla la mía. 
Que en el jardín de mi casa 
nunca falte la alegría. 

Ya no cantes cigarra, 
apaga tu sonsonete, 
que llevo una pena en el alma, 
que como un puñal se me mete 
sabiendo que cuando canto 
suspirando va mi suerte. 

Bajo la sombra de un árbol 
y al compás de mi guitarra 
canto alegre este huapango, 
porque la vía se acaba 
y no quiero morir soñando, 
ay, como muere la cigarra. 

Ábreme la puerta 
que vengo najando, 
y los gachés, primita de mi alma, 
sí a mí me ven 
me la van buscando. 

La vida, la vida, la vida es, 
es un contratiempo, 
la vida, la vida es. 

Ay la vida es, la vida es…

Una aplicación útil para la computación evolutiva

Cómo vimos en mi anterior artículo, la computación evolutiva tiene un enorme potencial que, en mi opinión, aún no ha sido suficientemente explotado. Y aunque es cierto que se utiliza con frecuencia para aplicaciones dentro de la inteligencia artificial, su uso podría llegar a ámbitos mucho más diversos. Me gustaría, por lo tanto, aprovechar esta entrada (ahora que ya tenemos una idea de lo que es la computación evolutiva), para mostraros un simple ejemplo práctico que demuestre la gran utilidad que este tipo de procesos computacionales puede tener:

Buscando patrones útiles.

Como ya vimos un ejemplo práctico de computación evolutiva y explicamos su funcionamiento interno, vamos a intentar darle una utilidad práctica a dicho ejemplo. En concreto, el programa de ejemplo era una aproximación numérica a la interpolación de una función desconocida a partir de un conjunto dado de datos.

Vamos por lo tanto a basarnos en esta cualidad del programa, para intentar encontrar patrones desconocidos a partir únicamente de ciertos datos empíricos conocidos. En muchas ocasiones, encontrar este patrón es imposible analíticamente, o si no es imposible, casi siempre es muy laborioso, requiriendo de complejos cálculos.

Un ejemplo de esto que digo puede ser el caso de intentar descubrir el patrón real que hay detrás del crecimiento de la población de un país. En el transcurso de los años, la población no crece o decrece de un modo aleatorio o caótico, sino que, a la vista de los datos, parece seguir cierto patrón o comportamiento. En principio este comportamiento del crecimiento de la población es desconocido, y sólo tenemos los datos empíricos de la población de un conjunto de años (los censos).

Según datos proporcionados por Funk & Wagnalls, el censo de Estados Unidos fue desde 1790 hasta 1990 el siguiente:

Realmente nos gustaría, a partir de estos datos, encontrar cual es el patrón oculto que dirige el crecimiento de la población para así, por ejemplo, poder estimar con cierta seguridad, cual será la población en el 2050 (año para el cual evidentemente aún no tenemos datos xD)

La búsqueda de este patrón es un ejemplo usualmente utilizado en la enseñanza universitaria para explicar al alumnado el concepto de ecuación diferencial. Pero para solucionar algún problema usando ecuaciones diferenciales, primero nos encontramos con el problema de conseguir modelar la situación usando ecuaciones en diferencia, luego nos encontramos con el problema frecuente de buscar el valor adecuado para los posibles parámetros usado en el modelo, y finalmente nos encontramos con el problema de encontrar una solución particular para esa ecuación diferencial a partir de ciertas condiciones iniciales.

Por ejemplo, mediante ecuaciones diferenciales se puede hacer un primer intento de modelado del patrón detrás del crecimiento de la población como este:

Este primer intento de modelo es fácil de calcular, y tiene, como solución analítica:

P(t) = 3.9 * e^(0.003067*t) 

pero cuando se contrasta esta función con los datos, vemos que el error cometido es grande a partir de cierto valor, por lo que finalmente no es un modelo que satisfaga el patrón oculto al crecimiento de la población.

¿Qué hacemos entonces? Pues buscar un nuevo modelo, solucionarlo y comprobar su nivel de aproximación con los datos.

Para este problema concreto, se suele utilizar un modelo llamado modelo logístico de la población, que viene a ser como el anterior, simplemente añadiendo un nuevo parámetro N que hace referencia a la capacidad de soporte del medio. De este modo, el modelo revisado es:

Esta ecuación diferencial ya no es lineal, y su resolución es más compleja, además de que ahora debemos conjeturar el valor de un nuevo parámetro N (además de k).

Este modo de actuar por ensayo y error de modelos es bastante complejo, laborioso y pesado. Para muchos problemas puede ser incluso un método inviable de actuación.

Resolución evolutiva.

¿Qué tal un método sencillo y universal? Un método que no requiera ni siquiera saber qué es una ecuación diferencial y que no necesite que tengamos que conjeturar con modelos para cada problema particular. Este método existe, y consiste simplemente, como seguro ya habréis podido imaginar, en el uso de un algoritmo de computación evolutiva.

La cuestión se reduce de este modo a introducir los datos empíricos en el programa, y a esperar a que el proceso evolutivo encuentre la función que mejor aproxime cada punto. Una vez alcanzada tal función con el nivel de aproximación especificado a priori, podemos estar seguro de que será una buena aproximación al patrón oculto a los datos empíricos de partida.

Posteriormente, simplemente tenemos que probar el patrón alcanzado con datos conocidos pero no pasados al programa (para asegurarnos de su fiabilidad), y finalmente, si la fiabilidad es buena, realizar predicciones para situaciones desconocidas utilizando este patrón hallado.

Aplicación práctica real al caso de estudio del crecimiento de la población de Estados Unidos.

Vamos a hacer uso de la aplicación que desarrollé para el artículo anterior. Como datos de entrada, vamos a introducir los datos facilitados por Funk & Wagnalls del censo de Estados Unidos desde 1790. Para poder estudiar la fiabilidad, no incluiremos las décadas posteriores a 1990. Por lo tanto la entrada del programa quedaría así:

{"x": 0} = 3.9;{"x": 10} = 5.3; {"x": 20} = 7.2; {"x": 30} = 9.6; {"x": 40} = 12;{"x": 50} = 17; {"x": 60} = 23; {"x": 70} = 31;{"x": 80} = 38;{"x": 90} = 50;{"x": 100} = 62;{"x": 110} = 75;{"x": 120} = 91;{"x": 130} = 105;{"x": 140} = 150;{"x": 150} = 131;{"x": 160} = 151;{"x": 170} = 179;{"x": 180} = 203;{"x": 190} = 226;{"x": 200} = 249;error_max = 10

Pulsamos en el botón "Ejecutar el proceso evolutivo" y esperamos las generaciones necesarias hasta que el error de interpolación de los puntos sea inferior a 10.

Cuando yo hice la prueba, el proceso terminó tras 271 generaciones, y me ofreció la siguiente función como resultado:

Es una función intimidante, ¿verdad? No te preocupes, es solo que el proceso evolutivo no busca, como puede hacer el científico humano, la sencillez algebraica. No la necesita. Y por eso esta función nos puede parecer extraña y difícil de entender. Pero es que realmente no necesitamos "comprender" el patrón encontrado, sino simplemente utilizarlo para realizar predicciones fiables con él.

Quizás este resultado sea después de todo una solución particular (o una aproximación) para el modelo logístico de la población que vimos antes, con un par de parámetros k y N desconocidos. O quizás no lo sea. No lo sabemos, pero tampoco lo necesitamos saber. Basta con que el patrón sea fiable.

¿El modelo encontrado es fiable?

Vamos a comprobarlo mediante su contrastación con otros datos conocidos pero que no han sido facilitados al programa.

El valor para las décadas posteriores a 1990 no fue facilitado precisamente con este propósito.

Pero primero veamos como se ajusta la función hallada a los datos facilitados al programa:

Año 1830 (t = 40): Valor predicho: 11,973 millones, Valor real: 12 millones, Error: 0,027
Año 1920 (t = 130): Valor predicho: 105,169 millones, Valor real: 105 millones, Error: 0,169
Año 1960 (t = 170): Valor predicho: 178,937 millones, Valor real: 179 millones, Error: 0,063

Se puede comprobar que existe un ajuste extraordinario.

Veamos, a continuación, cómo se ajusta la función a datos no facilitados al programa, pero que son conocidos empíricamente por otros medios. Como la tabla facilitada por Funk & Wagnalls no ofrece más información, usaremos otra fuente de datos alternativa. En concreto, vamos a usar los valores censales de Estados Unidos ofrecidos por la siguiente página web: http://www.datosmacro.com/demografia/poblacion/usa

Tenemos que tener en cuenta, sin embargo, un factor de corrección entre los datos facilitados por Funk & Wagnalls y los ofrecidos por la página web. Existe una variación entre las fuentes de datos de alrededor de un par de millones de habitantes de media. Por lo tanto, cuando usemos nuestra función para comprobar su fiabilidad con los datos de la web, debemos tener en cuenta estos 2 millones de diferencia (al alza o a la baja) entre losestimado por la función y el dato empírico ofrecido por la web datosmacro.

Teniendo esto en cuenta, hacemos las siguientes pruebas con datos no proporcionados al programa:

Año 1975 (t = 185): Valor predicho: 215,206, Valor real: 215,973 +- 2, Error: -0,767 +- 2
Año 1985 (t = 195): Valor predicho: 241,201, Valor real: 238,410 +- 2, Error: 2,791 +- 2
Año 1995 (t = 205): Valor predicho: 263,933, Valor real: 266,458 +- 2, Error: 2,525 +- 2
Año 2000 (t = 210): Valor predicho: 277,575, Valor real: 282,296 +- 2, Error: 4,721 +- 2
Año 2005 (t = 215): Valor predicho: 291,481, Valor real: 296,115 +- 2, Error: -4,634 +- 2
Año 2010 (t = 220): Valor predicho: 303,252, Valor real: 309,761 +- 2, Error: -6,509 +- 2
Año 2015 (t = 225): Valor predicho: 317,500, Valor real: 319,047 +- 2, Error: -1,547 +- 2

Teniendo en cuenta que gran parte del error cometido es probable que se deba al desajuste entre los datos de Funk & Wagnalls y los datos de la web, posiblemente el error medio cometido por la función cuando se contrasta con datos no usados en el proceso de interpolación esté alrededor de entre uno o dos millones. Este error medio, cuando hablamos de cientos de millones de personas, es bastante aceptable, y nos ayuda sin duda a hacernos una idea bastante ajustada de la población de Estados Unidos en cualquier año pasado o futuro (en el futuro será útil siempre que alguna catástrofe muy acusada no modifique el patrón seguido por el crecimiento real hasta ahora).

Predicciones futuras según el modelo.

¿Qué nos deparan las futuras décadas en cuanto a crecimiento de población en Estados Unidos se refiere? Pues, como digo, si no ocurren catástrofes apocalípticas no contempladas por el proceso tales como una epidemia o una guerra nuclear que aniquile a una gran parte de la población (modificando por lo tanto radicalmente el patrón real subyacente), el número de habitantes será con bastante seguridad el siguiente (con un error probable de un par de millones hacia arriba o abajo):

Año 2020 (t = 230): 332,981 millones de habitantes.
Año 2030 (t = 240): 354,429 millones de habitantes.
Año 2040 (t = 250): 387,272 millones de habitantes.
Año 2050 (t = 260): 425,315 millones de habitantes.
Año 2100 (t = 290): 526,467 millones de habitantes.
Año 2500 (t = 690): 3071,513 millones de habitantes.

Dentro de 5 años (ahora mismo estamos en el 2015), podremos comprobar la primera previsión y ver qué error cometió la estimación de nuestro modelo hallado ;).

Si se mantiene el patrón real seguido por Estados Unidos hasta ahora, vemos que pasarán muchas décadas antes de que alcance los 1000 millones de habitantes que tiene China hoy día.

Resumen.

Hemos visto un nuevo ejemplo del potencial que guarda la computación evolutiva. En este caso, hemos estudiado como ofrece una capacidad asombrosa en el descubrimiento de patrones ocultos; patrones que pueden ser demasiado complejos o caóticos para un estudio tradicional, pero que son perfectamente abordables mediante esta interesante y útil técnica de computación.

¿Qué es la computación evolutiva?

En esta entrada, que ya aviso que será un poco técnica, voy a intentar acercaros la base de lo que es una magnífica herramienta para la resolución de problemas de diversa índole. Me refiero, como no, a la computación evolutiva: la rama de la computación que hace uso del mismo proceso que la naturaleza ha seguido para conseguir fenómenos asombrosos que de otro modo serían totalmente inviables de alcanzar en un tiempo razonable. Por cierto, que gran parte de la moderna inteligencia artificial se basa en este precepto.

Introducción

Entendemos por un algoritmo evolutivo, aquel cuya técnica resolutiva se inspira en la evolución biológica de la naturaleza; imitando de esa manera, el proceso de selección natural que, desde Darwin, es aceptado como el principal motor del proceso evolutivo de los seres vivos.
Existe en la red abundante información teórica al respecto de la computación evolutiva, pero en muy pocos casos me he encontrado con ejemplos prácticos concretos, donde se pongan en práctica dichos principios.

De manera que me he propuesto intentar poner mi granito de arena práctico en esta rama tan interesante de la inteligencia artificial para ayudar así a cualquiera que quiera adentrarse en la materia.

Composición y funcionamiento de un algoritmo evolutivo (AE)

Sin duda, el mejor recurso bibliográfico para iniciarse en el mundo de la CE -compuactión evolutiva- es el magnífico libro Introduction to Evolutionary Computing, de los autores Agoston E. Eiben, y J.E. Smith.

Hemos dicho que la computación evolutiva es una ciencia computacional en la que sus algoritmos imitan el proceso evolutivo de la naturaleza. Veamos de qué partes consta, y cómo funcionan:

Cualquier AE seguirá el siguiente pseudocódigo:



Existe una población de n individuos, los cuales expresan una posible solución. La población es pues, un multiconjunto de genotipos, y forman la unidad de evolución.

Los individuos de la población se van renovando en sucesivas generaciones, que van convergiendo evolutivamente hacia la meta deseada, que no es otra que encontrar una solución a un problema determinado. La evolución se produce durante el paso de las generaciones, y cada generación cumple con el siguiente procedimiento:

La primera generación es especial, y sólo consiste en la generación (y evaluación) de una población inicial de n individuos, normalmente generados aleatoriamente.

El resto de generaciones comienzan con la selección de los individuos que se van a reproducir. Es decir, se seleccionan los padres que conformarán la descendencia.
Y dicha descendencia, será el resultado de un proceso de recombinación y mutación de esos padres previamente seleccionados. Tras la creación de la descendencia, se procede a evaluar su adaptabilidad. Es decir; se calcula, lo bien o mal que se adapta el nuevo individuo a las condiciones del medio ambiente. Este proceso se suele realizar, mediante el uso de una funcion de desempeño (fitness function). Dicha función representará la adaptabilidad del fenotivo expresado por el genotipo en cuestión. Una vez evaluada la progenie, se procede a seleccionar los individuos que finalmente prevalecerán para formar la siguiente generación.

Todo este proceso generacional, se repetirá mientras no se cumpla una condición de parada. La condición de parada normalmente será, o bien que uno o varios genomas expresan un fenotipo que es solución óptima del problema a resolver, o que se alcanzó el máximo de generaciones previstos programáticamente.

A continuación tenéis el programa con el que pondremos en práctica estas ideas. Podéis trastear un poco con él, y más tarde estudiar la explicación técnica del mismo:

Ejemplo VIII:

Podéis descargar el código fuente del ejemplo desde este enlace.

El algoritmo está escrito completamente en Javascript, utilizando hilos mediante la nueva clase Worker nativa de HTML5 (puedes descargar el código fuente desde el enlace de arriba):

Manual de uso

Mediante el algoritmo del ejemplo, vamos a intentar encontrar la solución óptima -si existe-, o la mejor aproximación posible, al siguiente problema:

Tenemos como entrada (inputs), una serie de puntos definidos para ciertos valores de una variable, y queremos buscar la función de interpolación que sea óptima -que pase por todos los puntos dados como entrada- o lo más aproximada posible.

Para introducir los inputs en el programa, debemos rellenar el campo de texto "Datos de interpolación", añadiendo cuantos puntos deseemos. Una entrada válida sería, por ejemplo:

{"x": 0} = 0;{"x": 1} = 3; {"x": 2} = 5.4142;{"x": 3} = 7.732;error_max = 0.001

Si ahora, pulsamos sobre el botón Ejecutar el proceso evolutivo, el programa se iniciará, buscando una de las muchas funciones que interpolan esos puntos, por ejemplo:

f(x) = 2*x + sqrt(x)

Para recalcar la potencia del proceso evolutivo por selección, se propone la posibilidad de intentar encontrar la solución, sin realizar la recombinación, mutación y selección de los más aptos, lo que resulta en un algoritmo completamente aleatorio que muy poco probablemente llegará a solucionar el problema.

Es importante señalar, que sólo se permite los operadores + - * /^, y que la prioridad de los mismos es la tradicional. Se permiten números con decimales (con el punto como separador, y una precisión máxima de cuatro decimales).

Al finalizar la ejecución del algoritmo, aparecerá una nueva zona en la aplicación con un par de gráficas, la primera representando los puntos de interpolación, y una segunda con los puntos representados por la función encontrada por el programa. Ambas gráficas coincidirán siempre y cuando se encuentre una solución óptima -si es que existe-.

Análisis del algoritmo

La representación del genotipo en nuestro ejemplo, consiste en un array de caracteres, conformando una cadena de texto, con los siguientes símbolos permitidos:{[0-9],x,+,-,/,*,^,sin,cos,sqrt,log}

Además, los símbolos deben respetar un patrón que forme cadenas con sentido aritmético (pero no se permite usar el símbolo - como operador unitario), permitiéndose genotipos como 2*x*x-1/2*x+23, pero no otros como 2+-x/*.

El AE del ejemplo responde al siguiente pseudocódigo:


t <- 0
Inicialización P(t)
Evaluación P(t)
hacer
S <- Seleccion_padres[P(t)]
Q = Operacion_variación[S]
Evaluación[Q)]
P(t+1) <- selección[P(t) U Q]
t <- t + 1
mientras no condición de parada


donde S, Q, y P son poblaciones de individuos, y t es una variable de tipo entera.

El algoritmo comienza creando aleatoriamente una población P de n individuos, y evaluando la función de desempeño de sus individuos -lo cerca o lejos que están de ser una solución óptima al problema-.

Posteriormente se entra en un bucle del que sólo se saldrá cuando se cumpla que, o bien en la población P(t) hay un individuo que es solución óptima, o bien se ha llegado al máximo de iteraciones previsto en la configuración del programa.

Cada iteración del bucle, se va a corresponder con una nueva generación de individuos, formada por parte de los padres de la generación anterior y por parte de su progenie.

Para realizar una generación se procede como sigue:

1) Se forma una población S con los individuos que van a poder procrear. En el caso concreto de mi ejemplo, todos los miembros de la población P van a tener descendencia. Es decir; S = P(t).

2) Se procede a crear la descendencia mediante recombinación, y mutación. En el ejemplo, se van seleccionando pares de individuos de S y se recombinan dando lugar a cuatro hijos.

Para recombinar, seleccionamos al padre y lo dividimos por un punto aleatorio p (quedando el padre partido en dos partes: padre1 y padre2). Hacemos lo mismo con la madre en un punto p', y se crean los hijos de la siguiente manera:

h1 = padre1 + madre2
h2 = madre1 + padre2
h3 = padre1
h4 = padre2

Posteriormente, cada hijo, sufrirá -con 100% de probabilidad- algún tipo de mutación puntual, que podrá ser más o menos leve, y que podrá modificar algún valor concreto del genotipo del individuo, o añadir o eliminar partes del mismo.

El proceso de reproducción, se repetirá 16 veces por cada par de padres, lo que dará un total de n*16*4 hijos en cada generación -siendo n el número de individuos en la población-.

3) El siguiente paso es evaluar la adaptabilidad de esta población Q que conforman la nueva descendencia.

4) Por último, se procede a seleccionar aquellos individuos que mejor se adaptan al medio de la unión del conjunto de padres de la generación anterior P(t) y el conjunto de sus hijos Q. Como resultado, se obtiene el conjunto P de la generación siguiente, con los supervivientes del proceso de selección.

En nuestro ejemplo, la evaluación de un genotipo se procesa mediante la aplicación de una función de desempeño (fitness function) al mismo. En este caso, la función será el resultado de sumar la diferencia en valor absoluto entre g(x) y el input en dicho punto: abs(y-g(x)).

Un genotipo óptimo, será aquel cuya función de desempeño tenga valor 0.

Para el AE del ejemplo, la selección generacional, se hace ordenando los individuos de [P(t) U Q] según su valor de adaptación -cuanto menos diferencia entre g(x) y los puntos de interpolación mejor- y seleccionando los s primeros, desechándose de esa manera el resto.

Resumen

El algoritmo evolutivo propuesto es capaz de encontrar; si existe, una solución óptima al problema con bastante frecuencia, aunque; como en todo AE existe la posibilidad de que la evolución generacional se localice en torno a una solución local no óptima -pero muy cercana de serlo-. Sin embargo, la aleatoriedad de la fase de mutación, permite teóricamente recomenzar un nuevo camino evolutivo en cualquier momento -aunque es menos probable que esto ocurra conforme pasan las generaciones-.

Aprendizaje funcional automático

Hace poco, mi hija comenzó en el colegio a aprender a realizar sumas de una cifra. Me resultó muy interesante observar el proceso que siguió para conseguirlo: ni más ni menos que un refuerzo paulatino de aprendizaje por ensayo y error. Esto me recordó un ejemplo de aprendizaje automático por ordenador que realicé hace ya años, y me propuse hacer algo similar adecuándolo al modo en que parece que mi hija ha conseguido aprender a sumar. El resultado lo tenéis a continuación.

Simulando los procesos neurológicos:

El campo más prometedor en IA desde hace décadas, es la simulación neuronal del cerebro animal mediante redes neuronales artificiales. Mediante esta simulación se han conseguido los avances más espectaculares en el terreno de la inteligencia artificial. Baste nombrar uno de los avances más notorios conseguidos por un equipo de desarrollo de Google, donde han conseguido que una única red neuronal artificial sea capaz de aprender de manera autónoma a jugar a 43 juegos diferentes y con un nivel de habilidad mayor al alcanzado por la media de personas. La red neuronal recibe como entrada únicamente los píxeles de colores de la pantalla del juego, y resuelve el modo en que hay que pulsar los distintos botones del mando para jugar bien.

Si este algoritmo se implantase en un robot con una cámara visual, y con "dedos" capaces de manipular un mando de videojuego, tendríamos el equivalente de un chaval jugando (de hecho, en realidad el robot jugaría a esos 43 juegos mejor que la media de chavales).

¿Y cómo se ha conseguido esta hazaña? Pues simplemente simulando por ordenador el funcionamiento de las neuronas del cerebro animal. Se crean nodos artificiales, que son el equivalente a las neuronas biológicas, y se unen unos con otros mediante enlaces o pesos wij (que son el equivalente a las interconexiones sinápticas entre neuronas naturales). Al igual que las neuronas, los nodos artificiales poseen un umbral de activación y un nivel de transmisión o inhibición similar al voltaje que una neurona emite y transmite mediante las dendritas.

Y aunque parezca ser una simulación complicada, en realidad computacionalmente es algo muy sencillo de hacer...¡y funciona!

Reforzando la red neuronal:

Una red neuronal artificial por sí sola no sirve de gran cosa. Si sus pesos y valores de umbral y transmisión contienen cualquier valor posible, la salida que produzca será aleatoria y sin sentido. no será funcional. Es necesario reforzar o entrenar esta red, de modo que se puedan ajustar los pesos y umbrales del modo adecuado para que la red neuronal pueda realizar una función útil.

Existen varios modos de ajustar una red neuronal, pero sin duda la más eficiente y sencilla, al menos en mi opinión, es mediante el uso de un proceso evolutivo.

Simplemente se trata de poner a prueba un gran conjunto de redes neuronales similares, y de ir seleccionando aquellas que mejor aproximen el resultado deseado. En cada generación se crearán nuevas redes a partir de las anteriores, las cuales podrán sufrir leves variaciones en sus parámetros (mutaciones). Esta simple iteración permite ajustar cualquier red neuronal de un modo eficiente para conseguir el fin deseado.

¿Aprendemos nosotros de un modo parecido?:

Tras estudiar el modo en que mi hija aprendió a sumar, yo creo, sin duda, que siguió un esquema muy similar al indicado arriba. Personalmente, creo que una gran parte (si no todo) del aprendizaje no instintivo que consiguen los animales (ser humano incluido), sigue un proceso de refuerzo por ensayo y error sobre un conjunto concreto de neuronas de nuestro cerebro.

Durante millones de años, el proceso evolutivo biológico habría sentado la base neuronal y la plasticidad necesaria para ajustar partes independientes de la masa neuronal para poder, literalmente, reforzar o inhibir las interconexiones y los umbrales de las neuronas de modo que se puedan conseguir salidas funcionales parciales. De este modo, el cerebro sería capaz de poseer cientos de miles de heurísticos (algoritmos) independientes pero conectados, los cuales darían lugar a toda la conducta en su complejidad.

El proceso de aprendizaje (aproximado y simplificado) que probablemente siguió mi hija pudo ser el siguiente:

Los números llegaron a su cerebro en forma de impulsos eléctricos gracias al sentido de la vista. Posiblemente algún heurístico innato (o varios) convirtieron y separaron esos impulsos en entradas para un determinado subconjunto neuronal concreto, el cual produjo una salida que otros heurísticos transformaron en un acto conductual: escribiendo la salida en un papel o diciendo en voz alta la respuesta. Cuando la respuesta fue correcta, nuestra aprobación (o la del profesor) llegó a su cerebro en forma de refuerzo positivo mediante los sentidos de la vista y el oído, y el subconjunto neuronal que se encargó de la tarea se vio reforzado. Cuando la respuesta fue errónea, le indicamos cual era la solución correcta, la cual llegó también a su cerebro y alteró a continuación el ajuste del subconjunto neuronal implicado en este asunto. En el momento que la salida del subconjunto fue  ya siempre correcta, no se recibieron nuevas correcciones, y el aprendizaje habría terminado.

Un nuevo heurístico ha aparecido en el cerebro de mi niña: ahora ya es capaz de sumar :).

El movimiento se demuestra andando:

Como es habitual, no me voy a quedar en la simple teoría, y voy a poner en práctica todo lo dicho mediante un ejemplo que yo mismo he desarrollado, y que podréis probar a continuación desde vuestro propio navegador:

Mediante un proceso de computación evolutiva, veremos como una red neuronal artificial de sólo 40 nodos, es capaz de aprender de manera autónoma a realizar sumas de una cifra (el aprendizaje es autónomo en el sentido de que en ningún momento al algoritmo se le indica cómo hay que sumar, y ni siquiera se le pasan los números en formato decimal. Tampoco se ajusta manualmente en modo alguno las variables de la red neuronal).

Técnicamente hablando, he utilizado una red neuronal con conexión hacia delante y una capa oculta (hidden layer). La capa de entrada contiene 20 nodos que se inicializan a 1 ó 0 según sea el input de entrada (el par de números a sumar). Cada nodo de la capa de entrada se une a cada nodo de la capa intermedia (la cual consta de otros 20 nodos), lo que da un total de 400 enlaces (pesos wij). Un último nodo de salida es el responsable de devolver el resultado del proceso neuronal expresando con su nivel de activación el resultado de la suma .

Inicialmente, los pesos wij de la red neuronal son marcados aleatoriamente, por lo que la respuesta de la red neuronal ante el problema será también aleatoria y casi siempre errónea. Hay pues que entrenar la red para que aprenda a evaluar bien la entrada, lo que vamos a conseguir ajustando evolutivamente los pesos de la red neuronal utilizada, el umbral de activación de cada nodo, y el nivel de transmisicón o inhibición asociado. Dicho entrenamiento evolutivo se realizará mediante una estrategia evolutiva.

Comenzamos con una población de 750 redes neuronales aleatorias (n = 750 individuos). Cada generación producirá n nuevos individuos que podrán sufrir una variación exclusiva por mutación -sin recombinación- y cuya función de desempeño (fitness fuction) será calculada mediante competición -selección por torneo-. Para el proceso de mutación, hay que tener en cuenta que cada individuo; además de un vector de pesos, contiene un vector de variables de ajuste (umbral de activación y valor de transmisión), que también irá evolucionando junto con los pesos. La mutación es de la forma:

Con alpha igual 0.2f, y donde xi indica el peso en la posición i del vector de pesos, y N(0,1) indica un valor tomado aleatoriamente de una distribución normal de desviación típica igual a 1, y media igual a 0. La otra variable que interviene en el proceso se corresponde con la variable de ajuste del elemento i, que; como se puede ver, muta antes de que lo haga el peso xi. La evaluación de un individuo se realiza mediante q pruebas (con q = 100) en donde se comprueba la capacidad del individuo para resolver las 100 combinaciones posibles en que se pueden sumar dos números en el dominio [0-9]. En el paso final de cada generación, se seleccionan aquellos n individuos que mejor han aproximado su respuesta ante las q sumas.

A continuación podéis probar este ejemplo de computación evolutiva que he desarrollado. Para alcanzar un aprendizaje completo, ajusta el campo "Número de generaciones para el aprendizaje" al menos en 150, en lugar de 50 como lo he puesto por defecto. Con el botón "Realizar prueba" podrás probar la funcionalidad de la mejor red neuronal alcanzada tras finalizar el proceso evolutivo:



Podéis descargar el código fuente del ejemplo desde este enlace.

El poder del proceso evolutivo:

Es interesante notar la enorme eficiencia y capacidad que tiene la computación evolutiva para encontrar, dentro de un gigantesco conjunto de posibilidades, los valores adecuados para conseguir un fin concreto. En este ejemplo que estamos estudiando, las combinaciones y los valores posibles para los pesos wij de los 400 enlaces, así como para los umbrales de activación y los valores de transmisión son astronómicos. Para que un proceso aleatorio consiguiese ajustar finamente estos valores de modo que la red neuronal pudiese sumar correctamente, probablemente harían falta cientos de miles de años, y sin embargo, el algoritmo evolutivo lo consigue en unos pocos minutos.

Física moderna

"Los fenómenos físicos se propagan como ondas e interaccionan como partículas" (Física para la ciencia y la tecnología de Tipler Mosca Vol.2C, pág. 1051)

Hace ya meses que me propuse alcanzar el estado del arte (o estado de la ciencia) en física. Aprovechando las pasadas vacaciones de semana santa he dado un nuevo empujoncito, y hoy he terminado de estudiar a fondo el temario sobre física moderna del libro recomendados por la UNED: Física para la ciencia y la tecnología de Tipler Mosca Vol.2C. Este libro es el recurso aconsejado para preparar la asignatura de segundo curso del grado de física: Fundamentos de física III.

Yo llevo muuuchos años leyendo y estudiando divulgación de física, pero hasta este momento, nunca había bajado a un nivel cuantitativo del temario que se trata en esta asignatura: Mecánica cuántica, relatividad y estructura de la materia. Realmente me ha impresionado.

Cuando me preparo una asignatura del grado de física de la UNED, lo hago como si realmente estuviese matriculado y fuese a hacer el examen (aunque por motivos económicos no puedo, ni quiero, gastarme un pastón en pagar por créditos que no me van a servir para nada). Me estudio el temario en varias de las referencias recomendadas, hago los ejercicios, e incluso realizo los exámenes de otros años para comprobar que he alcanzado el nivel requerido académicamente para superar la asignatura en esta Universidad.

Ahora mismo se podría decir que tengo el nivel de un alumno que ha aprobado todo el primer curso y comienza el segundo, De hecho, esta asignatura que comento es la primera que me preparo del segundo curso...y me ha gustado.

Hasta ahora he estado leyendo y estudiando las asignaturas de primero con no demasiado entusiasmo; en gran parte porque el temario tratado en ellas ya lo conocía en mayor o menor medida (por las asignaturas de física y electrónica que ya estudié cuando hice la ingeniería), y si acaso, lo que he hecho es profundizar matemáticamente en ciertos aspectos, pero poco más. Sin embargo, ahora realmente estoy disfrutando de este reto que me he propuesto. He visto que el objetivo final de estar al día sobre el conocimiento físico disponible del mundo no es tan distante, y que el camino que me queda es bastante interesante ;).

Realmente me siento un privilegiado por ser capaz de disfrutar mientras aprendo.