Voy a continuación a traduciros un interesante paper con fecha de junio de este año 2020. Los comentarios [entre corchetes] son anotaciones mías.
===================================================================================================
La inmunidad protectora del coronavirus es de corta duración.
Autores
Arthur WD Edridge 1 , Joanna Kaczorowska 1 , Alexis CR Hoste 2 , Margreet Bakker 1 , Michelle Klein 1 ,Maarten F. Jebbink 1 , Amy Matser 3 , Cormac M. Kinsella 1 , Paloma Rueda 2 , Maria Prins 3,4 , Patricia Sastre 2 ,Martin Deijs 1 , Lia van der Hoek *
Afiliaciones
1. Laboratorio de Virología Experimental, Departamento de Microbiología Médica y Prevención de Infecciones,Instituto de Infección e Inmunidad de Amsterdam, Amsterdam UMC, Universidad de Amsterdam, Meibergdreef 15,1105 AZ Amsterdam, Países Bajos.
2. INGENASA, Inmunología y Genética Aplicada SA, Av. de la Institución Libre de Enseñanza, 39, 28037Madrid, España
3. Departamento de Enfermedades Infecciosas, Servicio de Salud Pública de Amsterdam, Nieuwe Achtergracht 100, 1018.WT Amsterdam Países Bajos.4. Amsterdam UMC, Universidad de Amsterdam, Departamento de Enfermedades Infecciosas, Infección y AmsterdamImmunity Institute, Amsterdam UMC, Universidad de Amsterdam, Meibergdreef 15, 1105 AZ Amsterdam,Los países bajos.
ABSTRACT
En la pandemia actual de COVID-19, una pregunta clave sin resolver es la duración de la inmunidad adquirida en individuos recuperados. La reciente aparición de SARS-CoV-2 impide un estudio directo sobre este virus, pero cuatro coronavirus humanos estacionales pueden revelar características comunes aplicables a todos los coronavirus humanos.
Monitoreamos sujetos sanos durante un período de 35 años (1985-2020), proporcionando un seguimiento total de 2473 personas/meses. Se determinó: a) el tiempo de reinfección por cada cepa de coronavirus, y b) la evolución en la disminución de anticuerpos contra estos coronavirus tras la infección y posterior recuperación. Como resultado se encontró una alarmante corta duración en la inmunidad protectora frente a dichos coronavirus. Ocurrieron reinfecciones frecuentemente transcurridos 12 meses tras la enfermedad, y hubo, para cada virus, una reducción sustancial en los niveles de anticuerpos en un tiempo tan temprano como 6 meses.
TEXTO PRINCIPAL
El SARS-CoV-2 es un nuevo coronavirus responsable de la pandemia en curso. Su rápida transmisión es probablemente causada por el hecho de que el virus entró en un ser humano muy desprotegido y por lo tanto altamente susceptible de ser infectado, combinado con la capacidad del propio virus para transmitirse durante la fase asintomática de la infección.
Como no hay intervenciones farmacéuticas disponibles actualmente, las políticas actuales para limitar la propagación del SARS-CoV-2 gira en torno a la contención, el distanciamiento social y la suposición de que los pacientes recuperados desarrollan inmunidad protectora. La duración de la protección afectará no solo el curso general de la pandemia actual, sino también el período posterior a la pandemia misma. Hasta la fecha no hay evidencia concreta de reinfección por SARS-CoV-2, ni tampoco ningún ejemplo de reinfección por SARS-CoV-1 o MERS-CoV; sin embargo, esto es probablemente debido a la reciente aparición de SARS-CoV-2 y a la poca escalada infectiva que tuvo el SARS-CoV-1 y MERS-CoV [que no llegaron a convertirse en pandemia]. En general todos suponen que sí puede ocurrir una reinfección por cualquier tipo de coronavirus, sin embargo, esta tesis se funda de momento en un único estudio experimental sobre individuos voluntarios en donde se usó un coronavirus cultivado (HCoV-229E) inoculado en intervalos de 12 meses. Por lo tanto, debemos señalar que la susceptibilidad a la reinfección natural por coronavirus no ha sido investigada hasta ahora a fondo. Se suponen que las reinfecciones son posibles y que probablemente son dictadas por dos variables: la exposición al virus y la duración de la inmunidad adquirida tras la primera infección.
Actualmente no es posible investigar las reinfecciones por SARS-CoV-2 ya que estamos en una fase temprana de la pandemia, sin embargo los coronavirus estacionales [causante del resfriado común] pueden servir como modelo de estudio [dada la similitud silogenética entre los mismos y el SARS-CoV-2]. Hay cuatro especies de coronavirus estacionales: HCoV-NL63, HCoV-229E, HCoV-OC43 y HCoV-HKU1. Todos están asociados con infecciones leves del tracto respiratorio, pero los cuatro virus son genética y biológicamente diferentes. Dos pertenecen al género Alphacoronavirus , y dos al género Betacoronavirus [mismo género del SARS-CoV-2]. Los virus usan diferentes moléculas receptoras para ingresar a una célula objetivo, y en función de la distribución del receptor, no todas ingresan al mismo tipo de células epiteliales en los pulmones. Dada esta variabilidad, los coronavirus estacionales son los grupos de virus más representativos del cual concluir características generales de los coronavirus en cuanto a denominadores comunes como la dinámica de la inmunidad y la susceptibilidad a la reinfección.
El objetivo de este estudio es investigar la duración de la protección del coronavirus contra las reinfecciones. Examinar las reinfecciones mediante la prueba del virus en el material respiratorio requiere la recolección de muestras respiratorias de voluntarios durante cada síntoma de resfriado común y, debido a que las reinfecciones pueden ser asintomáticas, también durante períodos sin síntomas, durante años seguidos. Este tipo de colecciones de muestras son difíciles de obtener. La alternativa es medir los aumentos en los anticuerpos contra un virus (serología), como un indicador de infección reciente. Esta opción es aplicable, ya que se ha determinado que los niveles de IgG para el coronavirus estacional: 1) solo aumentan después de una infección exitosa, 2) también aumentan con la infección asintomática, y 3) no aumentan después de un desafío viral fallido. Las muestras de sangre recolectadas a intervalos regulares en estudios de voluntarios durante décadas pueden servir posteriormente como material esencial para investigar la dinámica de la reinfección basada en una serología. En teoría, las pruebas de neutralización del virus pueden parecer el mejor ensayo serológico cuando se investiga la inmunidad protectora, sin embargo, existen limitaciones graves. Primero, no hay una línea celular que facilite la replicación de HCoV-HKU1 y, por lo tanto, no se pueden realizar pruebas de neutralización para este virus. En segundo lugar, las únicas cepas de virus cultivadas HCoV-229E y HCoV-OC43 disponibles son de la década de 1960 y están adaptadas al laboratorio, las cuales pueden no ser representantes adecuados de los virus en estado salvaje. En cambio, medir los niveles de anticuerpos dirigidos a proteínas virales usando, por ejemplo, ELISA, sí permitirá la prueba de reinfección para los 4 coronavirus estacionales. En este caso, se debe hacer una elección cuidadosa para el antígeno, considerando la compensación entre sensibilidad y reactividad cruzada en un ensayo serológico. Aunque la proteína Spike provoca anticuerpos neutralizantes, es la menos conservada dentro de una especie de coronavirus estacional, y disminuye la sensibilidad para detectar infecciones. En contraste, la proteína N, y específicamente su región C terminal (NCt), está significativamente más conservada y se ha encontrado como la proteína más inmunogénica, específica y sensible para controlar las infecciones por coronavirus estacionales [5–9].
Dinámica dela infección.
De un estudio de prospectivo realizado con hombres adultos (ver M&M, 10), se seleccionaron diez sujetos que participaron desde el inicio del estudio y al menos 10 años en seguimiento. Estos participantes no informaron ninguna enfermedad grave que pudiera haber influido en su inmunidad (ver descripción del estudio en M&M). El seguimiento de los sujetos con recolección y almacenamiento de sangre comenzó en 1985 y, dejando de lado una brecha en el seguimiento entre 1997 y 2003, continuó para la mayoría de los sujetos hasta el 2020 a intervalos regulares (cada 3 meses antes de 1989 y cada 6 meses después). El período acumulativo en el que los sujetos fueron seguidos continuamente (es decir, < 400 días de intervalo entre muestras consecutivas) totalizó más de 200 años-persona = 2473 meses. Al comienzo del estudio, la edad de los sujetos varió de 27 a 40 años; Al final del seguimiento, los sujetos tenían entre 49 y 66 años.
Figura 1 - Dinámica de anticuerpos para coronavirus estacionales y virus del sarampión en el tiempo. (a) Dinámica de anticuerpos del sujeto 9. Los puntos conectados indican intervalos de seguimiento < 400 días. Los asteriscos significan visitas clasificadas como infecciones, el número adyacente al asterisco describe el cambio de pliegue observado en la densidad óptica del ELISA. (b) Distribución de cambios de pliegue OD entre visitas secuenciales. Los gráficos muestran valores medios con el rango intercuartil (IQR), los picos se extienden hasta el rango después del cual las muestras se consideran valores atípicos (1.5 x IQR por debajo del primero o por encima del tercer cuantil). En rojo: HCoV-NL63; azul: HCoV-229E; verde: HCoVOC43; púrpura: HCoV-HKU1; naranja: coronavirus estacionales totales; gris: virus del sarampión. (c) La reactividad de anticuerpos a HCoV-NL63-NCt se asocia con la neutralización de HCoV-NL63. En rojo: dinámica de anticuerpos medida por ELISA; azul: disolución de neutralizadores.
Las infecciones por coronavirus se determinaron midiendo los cambios de pliegue en la densidad óptica (DO) en el reconocimiento de anticuerpos NCt entre dos visitas consecutivas (mostradas para un individuo [el 9] en la Fig. 1a y para todos sujetos en la figura complementaria (S1). Primero medimos la fluctuación natural entre visitas consecutivas en anticuerpos contra el virus del sarampión para los 10 sujetos suponiendo que el sarampión no ocurrió durante el seguimiento, ya que todos los sujetos fueron vacunados durante la infancia. Los cambios de pliegue en la OD del anticuerpo para el virus del sarampión variaron entre 0,85 y 1,28 (Fig. 1b). Luego se determinó un umbral para la infección por coronavirus utilizando la distribución del cambio de pliegue OD, suponiendo que durante la mayoría de los intervalos no se produjo infección por coronavirus y, por lo tanto, las infecciones aparecen como valores atípicos. La Figura 1b muestra que los aumentos de OD ≥1.4 veces fueron atípicos (Fig. 1b). Luego determinamos si estos criterios de infección serológica podrían deberse a enfermedades similares a la influenza (ILI) en el intervalo que precede directamente al aumento de anticuerpos. De hecho, la notificación de síntomas de ILI coincidió con un aumento ≥1.4 en los anticuerpos (prueba exacta de Fisher p = 0.031, tabla complementaria S1). Finalmente comparamos los resultados de ELISA de HCoV-NL63 con la disolución de neutralizadores para HCoV-NL63 en dos sujetos (# 5 y # 7, con tres infecciones). Las infecciones mostraron un aumento en la disolución de neutralizadores que acompañó al aumento ≥1,4 veces en los anticuerpos NCt (Fig. 1c).
Un total de 132 eventos [infecciones], que van de 3 a 22 por sujeto, se clasificaron como infecciones por coronavirus (Tabla 1). Se encontraron tiempos medios de reinfección de 33 (IQR 18-60), 31 (IQR 15-42), 27 (IQR 21-49) y 46 (IQR 36-68) para HCoV-NL63, HCoV-229E, HCoV- OC43 y HCoV-HKU1, respectivamente, y 30 (IQR 18-54) meses para todos los virus combinados (Fig. 2a). No hubo diferencia estadísticamente significativa entre las longitudes de intervalo de infección de los virus individuales (prueba de Kruskal-Wallis, P = 0,74). En algunos casos, las reinfecciones ocurrieron tan pronto como los 6 meses (dos veces para HCoV-229E y una vez para HCoV-OC43) y los 9 meses (dos veces para HCoV-NL63). El tiempo de reinfección más frecuente observado fue de 12 meses. Para las reinfecciones que ocurrieron a los 6 meses no observamos reducción en los anticuerpos entre infecciones (Fig. 2a, círculos blancos), sin embargo, para los tiempos de reinfecciones > 6 meses se encontraron reducciones en los niveles de anticuerpos entre dos infecciones (visibles como picos en la Fig. 1a y Complementaria Fig. S1).
La capacidad de detectar reinfecciones a corto plazo está limitada por el intervalo de muestreo. Sin embargo, es importante destacar que no se observó reinfección en la primera visita de seguimiento posterior después de un intervalo de 3 meses (Fig. 2a). Observamos varias reinfecciones en visitas posteriores con un intervalo de 6 meses, lo que sugiere que no ocurren reinfecciones dentro de los 6 primeros meses. Para examinar más de cerca esto, también observamos cambios < 1.4 veces menor en los anticuerpos directamente después de una infección, siempre bajo el supuesto de que los niveles de anticuerpos que no disminuyen adecuadamente después de la infección pueden ser un signo de otra infección. Como se muestra en la figura 2b, solo se encontraron cambios por debajo de 1 después de la infección con cada muestreo de 3 meses y, por lo tanto, podemos concluir con seguridad que el punto de tiempo de confianza más temprano para la reinfección es de 6 meses.
Figura 2. Características de infección y reinfección, y dinámica de anticuerpos menguantes para coronavirus estacionales. (a) El intervalo de tiempo entre reinfecciones. Los puntos blancos indican reinfecciones para las cuales no se pudo observar una disminución intermedia en los niveles de anticuerpos. Las líneas verticales negras describen los tiempos medios de reinfección. (b) Cambios en los niveles de anticuerpos después de la infección en relación con la duración del intervalo de seguimiento. Cada círculo representa una infección. El eje x describe el tiempo hasta la próxima visita de seguimiento posterior a la infección. El eje y describe el cambio en el nivel de anticuerpos en la visita posterior. Los círculos más grandes representan una mayor relación de aumento en los niveles de anticuerpos en la infección inicial. La línea horizontal indica el límite entre aumentos (> 1.0) o disminuciones (< 1.0) en los niveles de anticuerpos en la próxima visita de estudio. (c) Curva de Kaplan-Meier que muestra disminución de anticuerpos después de la infección (100%, 75% y 50%), detalles en M&M.
Dinámica de anticuerpos después de la infección.
La inmunidad protectora puede durar menos que el tiempo medido hasta la reinfección porque una reinfección también requiere exposición a un virus. Por lo tanto, el decaimiento en los niveles de anticuerpos puede ser un mejor marcador de la inmunidad menguante. Aunque los anticuerpos contra la proteína N por sí mismos no son neutralizantes, pueden considerarse como un representante del total de anticuerpos (ver comparaciones con la neutralización Fig. 1c). Analizamos la dinámica de la disminución de los anticuerpos NCt después de la infección, calculando el tiempo hasta que se produjo un retorno del 50%, 75% o del total de los niveles de anticuerpos a la línea de base (niveles de anticuerpos previos a la infección). La mayoría de los pacientes perdieron el 50% de sus anticuerpos anti-proteína NCt después de 6 meses, el 75% después de un año, y regresaron completamente a los valores basales 4 años después de la infección (Fig. 2c y Fig. Suplementaria S1).
Infecciones simultáneas.
Aunque nuestras pruebas ELISA que usan la parte C-terminal de la proteína N se diseñaron con precaución para ser específicas para cada virus individual, no podemos descartar que ocurra un cierto grado de reactividad cruzada de anticuerpos. Por lo tanto, investigamos con qué frecuencia coincidían las infecciones, ya que la reactividad cruzada puede haber llevado a un etiquetado falso de las infecciones. Observamos que las infecciones simultáneas con un Alfacoronavirus (HCoV-NL63 o HCoV-229E) junto con Betacoronavirus (HCoV-HKU1 o HCoV-OC43) eran raras, sin embargo, vimos que las infecciones por los Betacoronavirus HCoV-OC43 y HCoV-HKU1 a menudo coincidían (38,5%, tabla 2). Asimismo, para los Alfacoronavirus, las infecciones por HCoV-229E coincidieron con las infecciones por HCoV-NL63 en el 59.5% de los casos, y viceversa en el 44.9% de los casos. Por lo tanto, existe el riesgo de que sobrestimásemos el número de infecciones y, por lo tanto, volvimos a analizar los datos con una definición más estricta de infección, que incluye solo el aumento de los anticuerpos más fuertes inducidos por un Betacoronavirus o Alphacoronavirus en un momento determinado. Según esta definición, todavía encontramos intervalos de infección comparables a los datos originales (Fig. S2 suplementaria), con intervalos mínimos de infección tan cortos como 6 meses y reinfecciones frecuentes a los 12 meses, aunque el número de reinfecciones obviamente se redujo.
Estudiando los anticuerpos comunes contra todos los coronavirus.
En teoría, los anticuerpos inducidos por infecciones por coronavirus pueden tener amplias características de reconocimiento en común. Para examinar esto, realizamos un ELISA adicional en los 10 sujetos, esta vez utilizando la proteína N completa de SARS-CoV-2, para permitir la detección de anticuerpos ampliamente reconocidos en coronavirus. Para excluir que la detección de este tipo de anticuerpos fueron falsos positivos debido a que fueron dirigidos a la etiqueta his en nuestras proteínas N de coronavirus, también realizamos un ELISA de control con una proteína de envoltura de VIH-1 etiquetada con his. Un sujeto (# 2) mostró un reconocimiento no específico, ya que también se reconoció la proteína VIH-1-SOSIP etiquetada con his (Figura complementaria S3). Otros dos sujetos mostraron anticuerpos ampliamente compartidos, muy probablemente inducidos por infecciones con Alphacoronavirus y Betacoronavirus durante el mismo intervalo (sujetos 9 y 10, Suplemento Fig. S3). Es de notar que no parece que estos anticuerpos compartidos sean buenos protectores ya que las infecciones por HCoV-NL63, HCoV-229E y HCoVOC43 ocurrieron en presencia de estos anticuerpos (Figura complementaria S1).
Infecciones por coronavirus según las estaciones del año.
Hasta la fecha, no está claro si el SARS-CoV-2 compartirá el mismo pico de prevalencia invernal que se observa en los coronavirus estacionales en países no ecuatoriales. Sin embargo, es importante considerar que la preferencia invernal de los coronavirus estacionales solo se ha determinado analizando muestras respiratorias de personas que experimentaron la enfermedad. Por lo tanto, el muestreo y el almacenamiento dependen de los síntomas y no del protocolo de estudio. Si la propagación del coronavirus continúa sin disminuir en verano, sin embargo, las personas rara vez muestran síntomas y, por lo tanto, no se toman muestras, las infecciones permanecerán sin ser detectadas. Nuestro estudio serológico es único porque evita este sesgo de muestreo. Los Países Bajos tienen un clima templado típico, y nuestras muestras de estudio fueron recolectadas a intervalos regulares. Las muestras de cada sujeto se distribuyeron aleatoriamente durante todo el año y, debido al régimen de visitas de 3 o 6 meses, se recolectaron muestras durante todas las estaciones. En consecuencia, podemos por primera vez visualizar la estacionalidad de las infecciones por coronavirus de manera imparcial. Estimamos la prevalencia de inicio de infección para cada mes para todas las infecciones detectadas en este estudio (ver los métodos suplementarios para detalles de análisis). Como se muestra en la Fig. 4, los meses de primavera y verano de mayo, junio, julio, agosto y septiembre muestran la prevalencia más baja de infecciones para los cuatro coronavirus estacionales (prueba de Wilcoxon de rango con signo, p = 0.005).
Fig. 4 Estacionalidad de las infecciones. Prevalencia de infección de los cuatro coronavirus estacionales en diferentes meses. La prevalencia por mes se muestra como un porcentaje del número total de infecciones por coronavirus.
DISCUSIÓN
Mostramos, por primera vez, que las reinfecciones por todos los coronavirus estacionales ocurren de manera natural. La mayoría de las reinfecciones ocurrieron en 3 años. Sin embargo, este intervalo de tiempo entre infecciones no indica que la inmunidad protectora de un individuo dure el mismo período de tiempo, ya que la reinfección también depende de la reexposición. De hecho, según los intervalos mínimos de infección y la dinámica de disminución de anticuerpos que observamos, la inmunidad protectora puede durar tan poco como 6 a 12 meses. Recientemente Kissler et al. modeló la inmunidad protectora y la dinámica de reinfección de los HCoV-OC43 y HCoV-HKU1 y estimó un período de inmunidad protectora de 45 semanas. Nuestro estudio serológico confirma esta predicción. Cuando vemos nuestros hallazgos a la luz de las acciones de control actuales tomadas para el SARS-CoV-2, queda claro que el riesgo de reinfección del coronavirus es clave para la política de salud pública. Aquí revelamos un riesgo de que en el futuro cercano, las pruebas basadas en serología que miden infecciones previas para el SARS-CoV-2 que usan la proteína N puedan tener un uso limitado si esa infección se produjo >1 año antes del muestreo. Nuestro estudio también muestra que la inmunidad colectiva puede ser un desafío debido a la rápida pérdida de la inmunidad protectora. Recientemente se sugirió que las personas recuperadas deberían recibir el llamado "pasaporte de inmunidad" que les permitiría relajar las medidas de distanciamiento social y proporcionar a los gobiernos datos sobre los niveles de inmunidad de rebaño en la población. Sin embargo, como la inmunidad protectora puede perderse a los 6 meses después de la infección, la posibilidad de alcanzar la inmunidad funcional del rebaño por infección natural parece muy poco probable.
Notamos que tres sujetos portaban anticuerpos que reconocían la proteína N del SARS-CoV-2 en ciertos puntos de tiempo. Es poco probable que hayan sido infectados con un virus similar al SARS-CoV-2 en 1985 (sujeto # 10), 1992 (sujeto # 2) o 2006 (sujeto # 9), y por lo tanto, sugerimos que estos anticuerpos ampliamente compartidos para hacer frente a los coronavirus han sido inducidos por infecciones coincidentes de un alfa y un betacoronavirus (en nuestros sujetos HCoV-HKU1 y HCoV-NL63). Para explorar este hallazgo, observamos la distancia genética y, en consecuencia, las diferencias de aminoácidos en la proteína estructural de los diversos coronavirus (tabla complementaria S2). La proteína N del SARS-CoV-2 tiene solo un 32% y 34% de coincidencia a nivel de aminoácidos con la proteína N del HCoV-OC43 y el HCoV-HKU1 respectivamente, y solo un 26% y 24% de identidad con HCoV-NL63 y HCoV-229E. De manera similar, la distancia entre el Alphacoronavirus y la proteína N del Betacoronavirus es grande (solo 24% a 26% de identidad entre aminoácidos). Aún así, no podemos excluir la presencia de epítopos conservados (conformacionales) en la proteína N del HCoV-HKU1 y el HCoV-NL63 que pueden dar como resultado una respuesta de anticuerpos de acción más amplia, debido a la exposición simultánea en infecciones concurrentes. Se requiere una evaluación adicional, que incluya más sujetos, para la confirmación.
No pudimos secuenciar el genoma del virus durante la infección. En teoría, la variación de la cepa podría jugar un papel en la susceptibilidad a la reinfección. HCoV-NL63, HCoV-OC43 y HCoV-HKU1 muestran diferentes grupos genéticos cocirculantes [4,14,15]. La situación es aún más complicada para HCoV-229E. Sylvia Reed ha demostrado que la reinfección experimental de voluntarios no tiene éxito cuando se usa la misma cepa de HCoV-229E, pero tiene éxito cuando se usan cepas heterólogas. Curiosamente, no se conocen subtipos genéticos importantes para HCoV-229E [17,18]. Como HCoV-NL63 no se conocía en la década de 1980, y las características del cultivo diferían entre las cepas HCoV-229E de Reed, las llamadas cepas heterólogas en realidad pueden haber sido HCoVNL63 [16,19]. Un estudio sobre inmunidad protectora idealmente permitiría la secuenciación de las cepas de reinfección de material respiratorio; sin embargo, esto es intratable en un estudio de infección natural porque la eliminación del virus en las reinfecciones puede ser tan breve como un día, y los esquemas de muestreo respiratorio serían extremadamente engorrosos para los voluntarios. Otra limitación del estudio es que los sujetos en nuestro estudio eran todos hombres. Para COVID-19, y también HCoV-NL63, los hombres tienen una mayor incidencia de la enfermedad [20] y, por lo tanto, es interesante determinar la dinámica de la inmunidad protectora también en una cohorte de mujeres sanas. En conclusión, todos los coronavirus humanos estacionales tienen poco en común, aparte de causar un resfriado común. Aún así, todos parecen inducir una inmunidad de corta duración con una rápida pérdida de anticuerpos. Este bien puede ser un denominador general para los coronavirus humanos.
Referencias
1. Callow, K. A. Efecto de la inmunidad humoral específica y algunos factores no específicos sobre la resistencia de voluntarios para la infección por coronavirus respiratorio. Epidemiology & Infection 95, 173-189 (1985).
2. van der Hoek, L. y col. Carga de la enfermedad debida a las infecciones por coronavirus NL63 humano y periodicidad de la infección. Journal of Clinical Virology 48, 104-108 (2010).
3. van der Hoek, L. Coronavirus humanos: ¿qué causan? Terapia antiviral 12, 651 (2007).
4. Pyrc, K. y col. Estructura mosaica del coronavirus humano NL63, mil años de evolución.
Journal of molecular biology 364, 964–973 (2006).
5. Dijkman, R. y col. El dominio de las infecciones por coronavirus humano OC43 y NL63 en lactantes. Journal of Clinical Virology 53, 135–139 (2012).
6. Cesantía, E. G. et al. Desarrollo de un inmunoensayo de coronavirus humano basado en nucleocápsides y estimaciones de individuos expuestos al coronavirus en una población metropolitana de EE. UU. Clínico y Vaccine Immunology 15, 1805-1810 (2008).
7. Sastre, P. y col. Diferenciación entre coronavirus humanos NL63 y 229E usando una novela
ensayo inmunosorbente ligado a enzimas sandwich de doble anticuerpo basado en un monoclonal específico anticuerpos Clinical and Vaccine Immunology 18, 113–118 (2011).
8. Dijkman, R. y col. Coronavirus humano NL63 y seroconversión 229E en niños. Journal of Clinical
Microbiology 46, 2368–2373 (2008).
9. Lehmann, C. y col. Una línea de inmunoensayo que utiliza proteínas nucleocápsides recombinantes para la detección de anticuerpos contra coronavirus humanos. Microbiología diagnóstica y enfermedades infecciosas 61, 40–48 (2008).
10. van Bilsen, W. P. H. y col. Tendencias divergentes en la incidencia del VIH versus otras enfermedades de transmisión sexual. Infecciones en HSH VIH negativos en Amsterdam. SIDA 34, (2020).
11. Gaunt, E. R., Hardie, A., Claas, E. C. J., Simmonds, P. y Templeton, K. E. Epidemiología y clínica presentaciones de los cuatro coronavirus humanos 229E, HKU1, NL63 y OC43 detectados en
años utilizando un nuevo método de PCR multiplex en tiempo real. Revista de microbiología clínica 48, 2940–2947 (2010).
12. Kissler, S. M., Tedijanto, C., Goldstein, E., Grad, Y. H. y Lipsitch, M. Proyectando la transmisión
dinámica del SARS-CoV-2 durante el período pospandémico. Ciencia (2020) doi: 10.1126 / science.abb5793.
13. Bendavid, E. y col. COVID-19 Anticuerpo Seroprevalencia en el Condado de Santa Clara, California. medRxiv 2020.04.14.20062463 (2020) doi: 10.1101 / 2020.04.14.20062463.
14. Woo, P. C. Y. y col. El análisis comparativo de 22 genomas de coronavirus HKU1 revela una novela genotipo y evidencia de recombinación natural en coronavirus HKU1. Revista de virología 80,
7136–7145 (2006).
15. Lau, S. K. P. y col. La epidemiología molecular del coronavirus humano OC43 revela la evolución de diferentes genotipos a lo largo del tiempo y la reciente aparición de un nuevo genotipo debido a la naturaleza recombinación Journal of virology 85, 11325–11337 (2011).
16. Reed, S. E. El comportamiento de aislamientos recientes de coronavirus respiratorio humano in vitro y en voluntarios: evidencia de heterogeneidad entre las cepas relacionadas con 229E. Revista de virología médica 13, 179-192 (1984).
17. Chibo, D. y Birch, C. Análisis de los genes de la espiga y nucleoproteína del coronavirus humano 229E demuestra la deriva genética entre cepas cronológicamente distintas. Revista de virología general 87, 1203-1208 (2006).
18. Farsani, S. M. J. y col. Las primeras secuencias completas del genoma de aislados clínicos de humanos coronavirus 229E. Virus Genes 45, 433–439 (2012).
19. van der Hoek, L., Pyrc, K. y Berkhout, B. Coronavirus humano NL63, un nuevo virus respiratorio. FEMS microbiology reviews 30, 760–773 (2006).
20. Kiyuka, P. K. y col. Coronavirus humano NL63 epidemiología molecular y patrones evolutivos en
Kenia costera rural. El diario de enfermedades infecciosas 217, 1728-1739 (2018).
"No hay que tomarse nada a pecho -se repite quien se enoja consigo mismo cada vez que sufre y no pierde ninguna ocasión de sufrir." El aciago Demiurgo (Emil Cioran)
martes, 28 de julio de 2020
viernes, 24 de julio de 2020
Charles Baudelaire: Embriagaos
«Embriagaos»
Hay que estar siempre ebrio. Todo se reduce a eso; es la única cuestión. Para no sentir el horrible peso del Tiempo, que os destroza los hombros doblegándoos hacia el suelo, debéis embriagaros sin cesar.
Pero, ¿de qué? De vino, de poesía o de virtud, como os plazca. Pero embriagaos.
Y si alguna vez os despertáis en la escalinata de un palacio, tumbados sobre la hierba verde de una cuneta o en la lóbrega soledad de vuestro cuarto, menguada o disipada ya la embriaguez, preguntadle al viento, a la ola, a la estrella, al pájaro, al reloj, a todo lo que huye, a todo lo que gime, a todo lo que rueda, canta o habla, preguntad qué hora es; y el viento, la ola, la estrella, el pájaro, el reloj os contestarán: «¡Es hora de embriagarse! Para no ser los esclavos martirizados del Tiempo, embriagaos; ¡embriagaos sin cesar! De vino, de poesía o de virtud, como os plazca.»
Charles Baudelaire. "Pequeños poemas en prosa o Spleen de París" (1862)
Un poema sencillamente maravilloso. Sobran las palabras.
jueves, 23 de julio de 2020
¿Existe realmente el bosón de Higgs?
Peso a lo que la gente cree, en el LHC lo que se "observó" NO fue en sí el fenómeno del Higgs, ya que esta partícula fundamental NO dura lo suficiente como para que un artilugio sea capaz de detectarla (su vida media es de 1.56×10^−22 segundos). Es decir, que ¡los detectores NO detectaron (valga la redundancia) un bosón de Higgs porque este desaparece (decae en otras partículas) casi tan pronto como aparece!, sino que se detectaron otras partículas más "mundanas" que no decaen o tardan lo suficiente en decaer como para llegar a alcanzar algún tipo de detector. En concreto, se puede detectar el rastro de: electrones, muones, taus, fotones, neutrinos, algunos mesones estables (quark-antiquark), algunos hadrones estables (conjunto de tres quarks como por ejemplo el protón y el neutrón), las anti-partículas de todas ellas...¡y nada más!
Es decir, que NO existen detectores de Higgs. El LHC no es especial en ese sentido. Y si se da por hecho la existencia del Higgs es porque se ha detectado una resonancia de las partículas "mundanas" antes descritas que cuadran con las matemáticas del modelo estándar:
Para que el modelo estándar fuera correcto, era necesario que el Higgs estuviera ahí; pero ante la imposibilidad de medirlo directamente, se tuvo que tirar de un "truco" estadístico (que ya se había utilizado antes en otras situaciones similares pero con partículas de menos masa: como los bosones W+- y Z, por ejemplo).
Ese "truco" no es ni más ni menos que el de variar poco a poco la energía de colisión de los hadrones e ir observando cuántos electrones se detectan, cuántos muones, etc. Pues bien, las matemáticas del modelo nos dice que, llegados a cierta energía, que concuerda precisamente con la de la masa de cualquier partícula que se quiera "descubrir" pero que no se pueda "ver" directamente, las gráficas estadísticas muestras un bump (un bulto o resalte) en la creación de partículas detectables.
Pues bien, en el LHC descubrieron una resonancia (un bulto en las gráficas) que era congruente matemáticamente (estadísticamente) con las predicciones del modelo estándar (adjunto imagen). Se dedujo de ello que se había descubierto al Higgs, y de camino se presupuso que ese bulto constituye la masa del mismo: ~125GeV.
EN RESUMEN:
"¿Existe el bosón de Higgs?" es una pregunta bastante mal planteada. NO existe ni (probablemente) existirá detector capaz de detectar directamente un Higgs o un quark, ni tampoco muchas otras partículas inestables. De hecho, las partículas "rastreables" de modo directo se cuentan con los dedos de las manos. Todas las demás se infieren de las matemáticas.
Así pues queda la duda de si esta inferencia matemática es capaz de dar cuenta de algún tipo de "existencia" o "realidad".
¿Qué opináis vosotros?
Es decir, que NO existen detectores de Higgs. El LHC no es especial en ese sentido. Y si se da por hecho la existencia del Higgs es porque se ha detectado una resonancia de las partículas "mundanas" antes descritas que cuadran con las matemáticas del modelo estándar:
Para que el modelo estándar fuera correcto, era necesario que el Higgs estuviera ahí; pero ante la imposibilidad de medirlo directamente, se tuvo que tirar de un "truco" estadístico (que ya se había utilizado antes en otras situaciones similares pero con partículas de menos masa: como los bosones W+- y Z, por ejemplo).
Ese "truco" no es ni más ni menos que el de variar poco a poco la energía de colisión de los hadrones e ir observando cuántos electrones se detectan, cuántos muones, etc. Pues bien, las matemáticas del modelo nos dice que, llegados a cierta energía, que concuerda precisamente con la de la masa de cualquier partícula que se quiera "descubrir" pero que no se pueda "ver" directamente, las gráficas estadísticas muestras un bump (un bulto o resalte) en la creación de partículas detectables.
Pues bien, en el LHC descubrieron una resonancia (un bulto en las gráficas) que era congruente matemáticamente (estadísticamente) con las predicciones del modelo estándar (adjunto imagen). Se dedujo de ello que se había descubierto al Higgs, y de camino se presupuso que ese bulto constituye la masa del mismo: ~125GeV.
EN RESUMEN:
"¿Existe el bosón de Higgs?" es una pregunta bastante mal planteada. NO existe ni (probablemente) existirá detector capaz de detectar directamente un Higgs o un quark, ni tampoco muchas otras partículas inestables. De hecho, las partículas "rastreables" de modo directo se cuentan con los dedos de las manos. Todas las demás se infieren de las matemáticas.
Así pues queda la duda de si esta inferencia matemática es capaz de dar cuenta de algún tipo de "existencia" o "realidad".
¿Qué opináis vosotros?
martes, 21 de julio de 2020
Guía paso a paso sobre cómo entrenar el modelo GPT-2 usando Google Colab
"Therefore the will has as its goal the mature consciousness of a man..."
(Schopenhauer GPT-2)
El modelo Schopenhauer-GPT-2 fue entrenado usando de base el modelo GPT-2 de OpenAI. Se realizó un fino ajuste sobre el modelo previamente entrenado al ser provisto de la obra completa del filósofo Schopenhauer. Este proyecto tiene como objetivo estudiar cómo GPT-2 puede comprender ideas y conceptos filosóficos profundos. Los resultados fueron bastante entretenidos y prometedores al presenciar como el modelo intenta siempre explicar y/o meter baza con el concepto Schopenhariano de Voluntad (the will). Os dejo un par de ejemplos del resultado final. El texto está en inglés puesto que el modelo pre-entrenado de partida es en inglés (de momento no hay versión en castellano):
"Therefore the will has as its goal the mature consciousness of a man, in which, therefore, in its nature, the perfection of itself may exist. Consequently, the development of this consciousness is in itself essential, and leads out of the man, not as something external to him, but merely as the product of his inner constitution. His will, upon the contrary, is conditioned by his intellect, and is the inner product of his intellect."
"The truth is, that the will really presents us with two problems: first, whether we should remain in ourselves, or whether, as soon as we set our selves, correctly, up as to our own individuality, we should, like other individuals, enter into relations of mingled freedom with a stranger. In the first place, the question is how we should go about this; secondly, how we should come to be ourselves again. The reply to the first is, that we ought to become what we were made to be—what each and all of us is—the will to live. The will is the first thing to recognize this truth."
Este proyecto, huelga decir, es fácilmente reutilizable para entrenar sobre otros textos y formatos. Podéis encontrar el código fuente aquí: https://github.com/Zeta36/schopenhauer_GPT_2
A continuación os dejo unas breves instrucciones para que podáis echarlo a andar con éxito:
Preparando su cuaderno de Google Colab
Utilizaremos Google Drive para guardar nuestros checkpoints (un checkpoint es nuestro último modelo guardado en el momento del entrenamiento). Una vez que se guarda nuestro modelo entrenado, podemos cargarlo cuando queramos generar textos condicionales e incondicionales.
Nota: no olvides configurar el tipo de ejecución de tu Google Colab en modo GPU.
Use el siguiente código para conectar tu Google Colab y tu Google Drive:
from google.colab import drive drive.mount('/content/drive')
Una vez conectado a Google Drive, creamos la carpeta donde almacenar los checkpoints:
%cd drive %cd My\ Drive %mkdir schopenhauer_gtp_2 %cd /content/ !ls
A continuación clonamos el repositorio GPT-2 de @Mohamad Ali Nasser
que es un fork del impresionante repositorio de @nnsheperd (que es a su vez un fork del repositorio original de OpenAI pero con la increíble incorporación del fichero de entrenamiento: train.py):
!git clone https://github.com/mohamad-ali-nasser/gpt-2.git
Ahora descargamos el modelo pre-entrenado que deseemos utilizar. Trabajaremos con el modelo '345M', que es bastante decente. La razón por la que trabajaremos con ese modelo en lugar de usar el '774M' o el '1558M' es porque la memoria de GPU disponible está limitada en Google Colab durante la fase de entrenamiento:
%cd gpt-2
!python3 download_model.py 345M
Ahora que el modelo está instalado, preparemos nuestro dataset y carguemos nuestros checkpoints en caso de que ya hayamos entrenado previamente nuestro modelo:
!ls /content/drive/My\ Drive/schopenhauer_gtp_2/checkpoint
!cp -r /content/drive/My\ Drive/schopenhauer_gtp_2/checkpoint/checkpoint/run1/* /content/gpt-2/models/345M
Descargar dependencias y CUDA.
Ahora que tenemos todo listo, preparemos el entorno. Comenzaremos instalando el archivo de dependencias.
%cd /content/gpt-2
!pip3 install -r requirements.txt
!pip install tensorflow-gpu==1.15.0
!pip install 'tensorflow-estimator<1 .15.0rc0="">=1.14.0rc0' --force-reinstall
!wget https://developer.nvidia.com/compute/cuda/9.0/Prod/local_installers/cuda-repo-ubuntu1604-9-0-local_9.0.176-1_amd64-deb
!dpkg -i cuda-repo-ubuntu1604-9-0-local_9.0.176-1_amd64-deb
!apt-key add /var/cuda-repo-*/7fa2af80.pub
!apt-get update
!apt-get install cuda-9-0
!export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/usr/local/cuda-9.0/lib64/
Entrenamos al modelo.
Ya podemos pasar directamente a entrenar al modelo utilizando el dataset (texto plano) que hayamos previamente decidido utilizar (en mi caso fue un archivo 'books.txt' con toda la obra completa de Schopenhauer en formato de texto):
!PYTHONPATH=src ./train.py --dataset /content/drive/My\ Drive/schopenhauer_gtp_2/dataset/books.txt --model_name '345M' --batch_size 1 --learning_rate 0.00001
El modelo guardará un checkpoint cada 1000 iteraciones. Puedes seguir ejecutándolo durante minutos, horas o días, todo depende de la cantidad de texto en el dataset.
Ahora que el modelo está entrenado, guardemos los checkpoints en Google Drive:
!cp -r /content/gpt-2/checkpoint/ /content/drive/My\ Drive/schopenhauer_gtp_2/checkpoint
Generando texto condicionado.
Finalmente ya podemos proceder a generar texto con nuestro nuevo modelo ajustado al dataset utilizado.
import os
%cd src
from conditional_model import conditional_model
%cd ..
conditional_model(seed=1, model_name='345M', sentences=['The truth is'])
Ésta última sentencia será la encargada de ofrecer una salida de texto generada por nuestro modelo completando el contexto pasado como parámetro (en el caso de ejemplo 'The truth is').
La salida, en mi caso; una vez entrenado GPT-2 con las obras completas del filósofo Schopenhauer fue el siguiente:
"The truth is, that the will really presents us with two problems: first, whether we should remain in ourselves, or whether, as soon as we set our selves, correctly, up as to our own individuality, we should, like other individuals, enter into relations of mingled freedom with a stranger. In the first place, the question is how we should go about this; secondly, how we should come to be ourselves again. The reply to the first is, that we ought to become what we were made to be—what each and all of us is—the will to live. The will is the first thing to recognize this truth."
Nota: Si queréis conocer más sobre el proyecto GPT-2 de OpenAI, podéis visitar esta entrada de su blog.
domingo, 19 de julio de 2020
Universos paralelos
"Cualquiera que no esté impactado con la teoría cuántica no la ha entendido."
(Niels Bohr)
Hace ya tiempo escribí varias entradas hablando sobre los conceptos más actuales de la física moderna. En la primera de dichas entradas hice una somera introducción al concepto de campo cuántico, base fundamental del conocido Modelo Estándar de partículas. En concreto, resulta que nuestra visión clásica de un Universo compuesto de átomos moviéndose por entre un espacio vacío es una mala aproximación y un símil que hace más mal que bien. Vamos a resumir a continuación brevemente el contenido de estas entradas antes de adentrarnos en la idea fundamental que queremos debatir en este artículo: los Universos paralelos.

A pesar de lo que siempre nos han contado, las partículas no son sustancias de naturaleza independiente, y tampoco se mueven por entre un vacío...puesto que el concepto de verdadero vacío no existe como tal. En realidad, se dice (y se conoce desde el siglo pasado) en jerga física que las partículas son realmente excitaciones de un campo cuántico. Y es cierto que es el hecho de utilizar estos extraños "palabros" precisamente lo que normalmente detiene a la divulgación científica de ir mucho más allá del concepto tradicional de átomo, pero vamos a intentar explicarlo a continuación de una manera sencilla y visual. No hay que tener miedo:
2) La física moderna nos cuenta que lo que en realidad existe (la sustancia básica) en el mundo no son partículas y vacío separándolas (i.e.; la vieja idea de Demócrito), sino campos como los arriba descritos. Estos campos esenciales son espacialmente infinitos e infinitesimales, llenando de este modo todo el espacio del Universo sin dejar hueco para un verdadero vacío. Cada campo es pues una especie de sustrato que se comporta como una colección infinitesimal de números que describen cada posición del espacio.
3) Existe como mínimo un campo cuántico por cada partícula conocida: así pues tenemos un campo para el electrón, el campo de Higgs, el campo del quark up, el campo del quark down, el campo del muón, etc.
4) Cada uno de estos campos se puede entender como si estuviesen compuestos por una infinidad de pequeños "muelles" unidos entre sí. De este modo podemos diferenciar dos tipos de "movimientos": el que hace cada muelle individual al vibrar (estirarse y contraerse a distinta velocidad), y el movimiento de traslación del conjunto de muelles conforme se alteran unos a otros mediante sus "impactos" (de manera similar a como una ola es el resultado ondulatorio de la agitación y vibración conjunta de cada molécula individual de agua).
5) Estos campos (los números que representan cada posición del espacio en realidad, como era el ejemplo de la temperatura de la cocina) presentan por lo tanto ondulaciones (cambios numéricos siguiendo funciones senoidales) que vibran a distinta intensidad, y que se trasladan por entre el espacio de manera similar a como el mar presenta olas de distintas alturas moviéndose a distinta velocidad por su superficie (aunque aquí como vemos lo que se mueve son valores numéricos siguiendo funciones matemáticas).
6) Pues bien: se entiende e interpreta desde la física (llevando quizás demasiado lejos a la metafórica) que la "altura" e intensidad de una onda dentro de un campo cuántico representa cuántas partículas del campo concreto existe en una posición concreta del espacio, mientras que la velocidad de traslación de dicha onda va a representar la energía (momento) que poseen estas partículas.
7) Y muy importante: una posición del espacio que no contenga ondulación alguna se dice que está en reposo (en su estado fundamental), pero que no está vacía. Es decir, que aunque NO existen partículas como tal puesto que no hay ondulaciones en el sentido del punto 6), sí que existe en cada posición infinitesimal del espacio esa sustancia (numérica) que conforma el propio campo y que aún en su estado fundamental presenta cierta vibración y potencial mínimo, remanente del principio de incertidumbre de la mecánica cuántica.
8) Las partículas de un cierto tipo son como vemos excitaciones ondulatorias del campo cuántico al que pertenecen, de manera que el sustrato y la sustancia del mundo no es la partícula en sí, sino esa especie de propiedad (numérica) ubicua que denominamos campo.
9) Finalmente comentar que los distintos campos interaccionan (se acoplan) entre sí dando como resultado lo que normalmente se conoce como fuerza. Es decir, que una fuerza no es ni más ni menos que el hecho de que una ondulación de cierto campo "tropezó" con una ondulación de otro campo distinto dando como resultado una perturbación que acaba modificando el estado de los campos implicados en el proceso.
10) El modo (probabilidad) en que los campos se acoplan entre sí (el resultado de las interacciones), además del modo en que las ondas de cada campo se mueven (su dinámica) vienen determinadas por las matemáticas de lo que se conoce como el modelo estándar de partículas. Estas matemáticas permiten determinar la fenomenología microscópica (calcular la manera en que los valores numéricos de los distintos campos van a variar) con una precisión de decenas de decimales.
En resumen:
La partícula "virtual" en física teórica es un término bastante confuso de partida, pero gracias al símil de los "mares" que venimos haciendo desde el principio podemos acordar que será "virtual" aquella partícula que no cumpla con un único requerimiento: esto es, que sea una perturbación en un "mar" (campo cuántico) pero que ¡no presente un movimiento estable, regular, suave y periódico!
Por lo tanto, partículas "reales" y "virtuales" son en esencia la misma cosa: perturbaciones y alteraciones en sus "mares" correspondientes las cuales alteran el estado fundamental de reposo ("mar" sin "olas" -o técnicamente, campo cuántico en su estado de vacío-). Siendo de remarcar que la única diferencia entre ambos fenómenos físicos es el hecho de que las partículas "virtuales" constituyen perturbaciones (alteraciones dinámicas) no periódicas, semi-caóticas, y abruptas que sin embargo acontecen en el mismo "mar" (campo cuántico) que las suaves perturbaciones (senoidales) capaces de permanecer y trasladarse como un flujo en dicho "mar" (las partículas "reales").
Interacción entre mares a base de partículas "virtuales".
Y es precisamente la función de las partículas "virtuales" la de perturbar los diferentes campos cuánticos según sean las propiedades intrínsecas que las partículas "reales" posean a la hora del acoplamiento efectivo. En el caso de dos electrones que se aproximan y repelen, visual y simbólicamente se podrían interpretar los hechos como sigue:
Empezamos con dos suaves y periódicas ondas ("olas") en el "mar" de electrones que se van moviendo y trasladando por el espacio (los puntos azules de la ilustración). El simple movimiento de cada electrón individual produce (debido a la carga eléctrica que transporta de manera intrínseca) una perturbación abrupta, caótica y no periódica en el "mar" de fotones (campo cuántico electromagnético). Estas alteraciones ("olas") no periódicas (no ondulatorias) ya vimos que no se mueven por el espacio y desaparecen casi tan pronto como aparecen: ¡son fotones "virtuales"!

Pero aunque las alteraciones -"virtuales"- en el "mar" de fotones no se trasladen como tal, el hecho es que siempre aparecen y desaparecen de manera contínua de modo que de todas formas una especie de "nube de fotones virtuales" siempre acompaña al electrón, siendo la probabilidad de que un electrón genere un abrupto fotón "virtual" en cierta posición x del espacio inversamente proporcional a la distancia entre el electrón y x (aunque el rango efectivo es en realidad infinito, y cualquier electrón puede generar con cierta probabilidad -cada vez menor- un fotón "virtual" a cualquier distancia no importa cuan lejos miremos). Por lo tanto, conforme más cerca de la suave onda del electrón nos coloquemos, más probable es que surja de manera espontánea una áspera perturbación en el "mar" de fotones. Así pues podemos imaginar esa suave onda periódica que se mueve (el electrón) rodeada de círculos concéntricos de fotones "virtuales" (perturbaciones que no son ondas, y que aparecen y desaparecen rápidamente) conformando una especie de "nube" cuya densidad disminuye conforme nos alejamos espacialmente del electrón.
Pues bien, cuando dos electrones se aproximan ocurre algo muy interesante. La densidad de fotones "virtuales" que acompañan a ambos electrones empiezan a armonizar y compaginarse de tal suerte que van dictando una dinámica muy particular para ambas partículas "reales". En el caso de que las cargas eléctricas sean iguales (como el caso de dos electrones) estas aditivas alteraciones (abruptas -"virtuales"-) en el "mar" de fotones determinará un flujo repulsivo contra la suave onda (perturbación ondulatoria en el "mar") del electrón, modificando de este modo su camino recto (el cual se habría visto inalterado de no ser por esta interacción con el "mar" de fotones).
Es decir, que las alteraciones ("los fuertes y caóticos oleajes") generados por cada electrón (debido a su carga) en el "mar" de fotones, son los que "empujan" las ondas de las partículas "reales" modificando su momento (sentido de movimiento y velocidad). ¡Es precisamente en este sentido en el que se dice que las partículas "virtuales" son las encargadas de transmitir las "fuerzas" en la naturaleza! De no ser por ellas, todas las partículas se moverían libremente sin interactuar unas con otras en modo alguno, y por lo tanto las trayectorias de éstas jamás se verían alteradas: todo iría siempre siguiendo el camino más recto posible...y punto.
El Modelo Estándar y sus interacciones.
El Modelo Estándar es el encargado de reunir matemáticamente todo lo explicado hasta ahora de modo que sea posible la predicción de fenómenos en física de partículas con alta precisión (de hecho, con la mayor precisión alcanzada hasta la fecha por la humanidad en un experimento). Para ello se vale del concepto abstracto del lagrangiano: grosso modo una función matemática como otra cualquiera, si no fuese por la particularidad que tiene de reflejar con congruencia el comportamiento de estos "mares" cuánticos y sus posibles interacciones.
Esta función matemática le costó a la humanidad más de 50 años de duro esfuerzo teórico antes de quedar en su forma actual. Esta fórmula logra describir de manera congruente la mayor parte del fenómeno del universo necesitando para ello de 12 partículas materiales (los fermiones, que aparecen siempre exclusivamente como partículas "reales"), y 6 partículas portadoras de la fuerza (los bosones, encargados de producir las interacciones entre los "mares" cuando aparecen como partículas "virtuales").
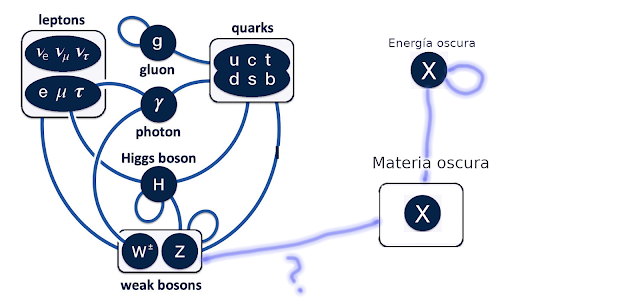
Hay cuatro fuerzas conocidas (interacciones) cada una mediada por una partícula fundamental intermediaria o portadora (un bosón actuando como partícula "virtual"): los fotones (interacción electromagnética como la del ejemplo anterior), gravitones (interacción gravitatoria), los gluones (interacción nuclear fuerte), y las partículas W± y Zº, portadoras de la fuerza nuclear débil.
A estas partículas simplemente hay que añadir el famoso bosón de Higgs, el encargado de dotar de masa a las partículas fundamentales (gracias a su interacción con casi todas las demás partículas).
Por último, por supuesto, debemos nombrar el famoso lagrangiano, la ecuación fundamental del modelo. Esta función intimida a primera vista, pero baste decir que toda esa álgebra simplemente es una manera de poder cuadrar los dos esquemas anteriores de modo que se pueda representar la dinámica de interacciones propuestas con el fenómeno observado al experimentar. Es una fórmula enrevesada y compleja, pero no hubo más remedio que hacerla así para que los datos numéricos fuesen congruentes. De todas formas no hay mucho más que una larga serie de sumas, restas, multiplicaciones y divisiones en ella. La aparente dificultad no es más que una ilusión debido a lo críptico de los símbolos utilizados:
El problema de la materia oscura y la energía oscura.
Merece la pena mencionar en este punto el problema existente actualmente con el desconocimiento sobre qué es la materia y la energía oscura. Sencillamente no se sabe qué son. Sin embargo, se puede atisbar la explicación más plausible: qué sean representaciones de nuevos campos cuánticos ("mares") aún no descubiertos. En este sentido, y si nos fijamos en el esquema anterior sobre las interacciones del Modelo Estándar, la mejor apuesta es que la materia oscura es un nuevo tipo de partícula material (partícula "real") que interacciona únicamente (o casi) mediante el intercambio de gravitones (fuerza gravitatoria) y no (o apenas) mediante el intercambio de ninguno de los demás bosones portadores de fuerza. De esta forma no habría manera de detectar ("ver) estas partículas oscuras más allá de la observación de sus efectos gravitacionales.
Por otra parte, la energía oscura se podría explicar mediante el uso de un campo cuántico "especial", similar al campo de Higgs o el hipotético inflatón. Estos campos actúan sobre lo que se entiende tradicionalmente como masa, y pueden hacer aparecer efectos extraños sobre el mismísimo espacio-tiempo (como es la aparición de una fuerza repulsiva que aumenta linealmente con el volumen del espacio).
En cualquier caso, lo importante del asunto es señalar que las matemáticas del Modelo Estándar permiten la existencia de más partículas fundamentales y más interacciones de las descritas hasta el momento. Sería, groso modo, tan "sencillo" como añadir y/o modificar miembros algebraicos en la estructura de la ecuación del lagrangiano.
Universos paralelos.
Y por fin llegamos a lo que se pretendía tratar desde un inicio en esta entrada: las matemáticas del Modelo Estándar también permiten de la existencia de uno (o varios) Universos que convivan de manera simultánea pero independiente con el nuestro. Sería éste el caso si la realidad contuviese campos cuánticos independientes (grafos inconexos); es decir, si existiesen otros grupos de campos cuánticos (partículas) sin interacción alguna entre sí (ni siquiera gravitatoria). Es decir, que muy bien podría existir un paquete independiente de campos cuánticos similares a los de nuestro día a día, pero con la particularidad de que no interaccionan con ninguno de nuestros bosones portadores de fuerza (ni siquiera con el gravitón).
Una manera sencilla de visualizar lo que acabamos de decir es suponer que existe de manera paralela a los campos descritos en el Modelo Estándar una especie de negativo inconexo de partículas y fuerzas. Tendríamos así las mismas partículas materiales y portadoras de fuerza pero no tendrían conexión ni interacción alguna con las de nuestro "mundo". Es decir, que no habría ningún punto de encuentro ni afectación entre estos campos y los del Modelo Estándar. ¡Tendríamos así "mundos" paralelos conviviendo en la misma región del espacio-tiempo! Y cada Universo tendría sus eventos causales y sus "seres" (fenómenos) autónomos. En estos hipotéticos (y posibles) mundos paralelos podrían incluso existir seres inteligentes como nosotros, los cuales habrían dado a sus campos cuánticos y fuerzas otros nombres, e incluso podrían sospechar de la existencia de nuestro Universo, como estamos nosotros haciendo aquí con el suyo.
Pero hay que dejar claro que esta tesis que defendemos no se limita a la posible existencia de uno o unos pocos Universos paralelos conviviendo literalmente con el nuestro, sino que debemos recalcar la posibilidad de que exista una infinidad de ellos todos actuando a la vez de manera concurrente pero desconectada. De hecho, esta idea podría servir de soporte al multiverso matemático del que nos habla el famoso físico Max Tegmark en su obra "Nuestro Universo matemático". Miles de billones de diversas estructuras matemáticas todas sucediendo en el mismo instante pero inconexas entre sí. Una infinidad de mundos paralelos donde únicamente aquellas estructuras con la complejidad necesaria para albergar vida consciente contendrá seres capaces de preguntarse por la propia estructura matemática que los sustenta (sus propiedades y su comportamiento fenoménico).
¡Es sorprendente que la física moderna permita (e incluso favorezca) la posibilidad de este tipo de hipótesis!
En resumen:
El Universo completo está lleno de varios tipos de "mares" (campos), y cada "mar" representa un tipo especial de partícula. Cuando cierto mar no presenta excitación alguna en una posición o lugar x, se dice que está en su estado fundamental y que allí NO hay partículas (aunque sigue habiendo "algo" -el campo- y no se puede decir que en x exista un verdadero vacío). Estos mares pueden presentar como decimos ondulaciones y flujos que se mueven vibrando por entre su ser. La velocidad de traslación y el modo de vibración individual del "agua" ("muelles" siguiendo un movimiento ondulatorio armónico simple) determinarán el momento y el número de partículas en cierta posición x.
La excitación ondulatoria en estos mares se puede traspasar o ceder de un tipo de mar a otro, lo cual constituye el hecho de que una excitación preexistente en cierto mar en la posición x, se pueda convertir en una excitación en otro mar distinto en ese mismo punto x, dando como resultado el equivalente a la aniquilación espontánea de un tipo de partícula y la aparición de otra. Pero en realidad como vemos no se trata de que nada salga de la nada o desaparezca en ella, sino que simplemente las excitaciones ondulatorias se transmiten con cierta probabilidad de un tipo de mar a otro.
Podemos así comprender que las 3 partículas estables que sabemos componen todo lo que vemos en nuestro día a día (electrones, quarks up y quarks down), no son otra cosa más que vibraciones ondulantes dentro de sus mares constituyentes (campos cuánticos). La materia se reduce de este modo a ondas de probabilidad (sinusoidales) moviéndose (numéricamente) dentro de ciertos sustratos cuánticos primordiales que embeben de manera ubicua al Universo por completo desde su mismo origen.
La materia es número, es función, cambio algebraico, ondulación y probabilidad...y poco más.
Partículas "virutales" y partículas "reales".
Por lo tanto, partículas "reales" y "virtuales" son en esencia la misma cosa: perturbaciones y alteraciones en sus "mares" correspondientes las cuales alteran el estado fundamental de reposo ("mar" sin "olas" -o técnicamente, campo cuántico en su estado de vacío-). Siendo de remarcar que la única diferencia entre ambos fenómenos físicos es el hecho de que las partículas "virtuales" constituyen perturbaciones (alteraciones dinámicas) no periódicas, semi-caóticas, y abruptas que sin embargo acontecen en el mismo "mar" (campo cuántico) que las suaves perturbaciones (senoidales) capaces de permanecer y trasladarse como un flujo en dicho "mar" (las partículas "reales").
Interacción entre mares a base de partículas "virtuales".
Y es precisamente la función de las partículas "virtuales" la de perturbar los diferentes campos cuánticos según sean las propiedades intrínsecas que las partículas "reales" posean a la hora del acoplamiento efectivo. En el caso de dos electrones que se aproximan y repelen, visual y simbólicamente se podrían interpretar los hechos como sigue:
Empezamos con dos suaves y periódicas ondas ("olas") en el "mar" de electrones que se van moviendo y trasladando por el espacio (los puntos azules de la ilustración). El simple movimiento de cada electrón individual produce (debido a la carga eléctrica que transporta de manera intrínseca) una perturbación abrupta, caótica y no periódica en el "mar" de fotones (campo cuántico electromagnético). Estas alteraciones ("olas") no periódicas (no ondulatorias) ya vimos que no se mueven por el espacio y desaparecen casi tan pronto como aparecen: ¡son fotones "virtuales"!

Pero aunque las alteraciones -"virtuales"- en el "mar" de fotones no se trasladen como tal, el hecho es que siempre aparecen y desaparecen de manera contínua de modo que de todas formas una especie de "nube de fotones virtuales" siempre acompaña al electrón, siendo la probabilidad de que un electrón genere un abrupto fotón "virtual" en cierta posición x del espacio inversamente proporcional a la distancia entre el electrón y x (aunque el rango efectivo es en realidad infinito, y cualquier electrón puede generar con cierta probabilidad -cada vez menor- un fotón "virtual" a cualquier distancia no importa cuan lejos miremos). Por lo tanto, conforme más cerca de la suave onda del electrón nos coloquemos, más probable es que surja de manera espontánea una áspera perturbación en el "mar" de fotones. Así pues podemos imaginar esa suave onda periódica que se mueve (el electrón) rodeada de círculos concéntricos de fotones "virtuales" (perturbaciones que no son ondas, y que aparecen y desaparecen rápidamente) conformando una especie de "nube" cuya densidad disminuye conforme nos alejamos espacialmente del electrón.
Pues bien, cuando dos electrones se aproximan ocurre algo muy interesante. La densidad de fotones "virtuales" que acompañan a ambos electrones empiezan a armonizar y compaginarse de tal suerte que van dictando una dinámica muy particular para ambas partículas "reales". En el caso de que las cargas eléctricas sean iguales (como el caso de dos electrones) estas aditivas alteraciones (abruptas -"virtuales"-) en el "mar" de fotones determinará un flujo repulsivo contra la suave onda (perturbación ondulatoria en el "mar") del electrón, modificando de este modo su camino recto (el cual se habría visto inalterado de no ser por esta interacción con el "mar" de fotones).
Es decir, que las alteraciones ("los fuertes y caóticos oleajes") generados por cada electrón (debido a su carga) en el "mar" de fotones, son los que "empujan" las ondas de las partículas "reales" modificando su momento (sentido de movimiento y velocidad). ¡Es precisamente en este sentido en el que se dice que las partículas "virtuales" son las encargadas de transmitir las "fuerzas" en la naturaleza! De no ser por ellas, todas las partículas se moverían libremente sin interactuar unas con otras en modo alguno, y por lo tanto las trayectorias de éstas jamás se verían alteradas: todo iría siempre siguiendo el camino más recto posible...y punto.
El Modelo Estándar y sus interacciones.
El Modelo Estándar es el encargado de reunir matemáticamente todo lo explicado hasta ahora de modo que sea posible la predicción de fenómenos en física de partículas con alta precisión (de hecho, con la mayor precisión alcanzada hasta la fecha por la humanidad en un experimento). Para ello se vale del concepto abstracto del lagrangiano: grosso modo una función matemática como otra cualquiera, si no fuese por la particularidad que tiene de reflejar con congruencia el comportamiento de estos "mares" cuánticos y sus posibles interacciones.
Esta función matemática le costó a la humanidad más de 50 años de duro esfuerzo teórico antes de quedar en su forma actual. Esta fórmula logra describir de manera congruente la mayor parte del fenómeno del universo necesitando para ello de 12 partículas materiales (los fermiones, que aparecen siempre exclusivamente como partículas "reales"), y 6 partículas portadoras de la fuerza (los bosones, encargados de producir las interacciones entre los "mares" cuando aparecen como partículas "virtuales").
Hay cuatro fuerzas conocidas (interacciones) cada una mediada por una partícula fundamental intermediaria o portadora (un bosón actuando como partícula "virtual"): los fotones (interacción electromagnética como la del ejemplo anterior), gravitones (interacción gravitatoria), los gluones (interacción nuclear fuerte), y las partículas W± y Zº, portadoras de la fuerza nuclear débil.
A estas partículas simplemente hay que añadir el famoso bosón de Higgs, el encargado de dotar de masa a las partículas fundamentales (gracias a su interacción con casi todas las demás partículas).
 |
| Esquema con todas las partículas del Modelo Estándar |
 |
| Esquema con todas las interacciones del Modelo Estándar |
El problema de la materia oscura y la energía oscura.
Merece la pena mencionar en este punto el problema existente actualmente con el desconocimiento sobre qué es la materia y la energía oscura. Sencillamente no se sabe qué son. Sin embargo, se puede atisbar la explicación más plausible: qué sean representaciones de nuevos campos cuánticos ("mares") aún no descubiertos. En este sentido, y si nos fijamos en el esquema anterior sobre las interacciones del Modelo Estándar, la mejor apuesta es que la materia oscura es un nuevo tipo de partícula material (partícula "real") que interacciona únicamente (o casi) mediante el intercambio de gravitones (fuerza gravitatoria) y no (o apenas) mediante el intercambio de ninguno de los demás bosones portadores de fuerza. De esta forma no habría manera de detectar ("ver) estas partículas oscuras más allá de la observación de sus efectos gravitacionales.
Por otra parte, la energía oscura se podría explicar mediante el uso de un campo cuántico "especial", similar al campo de Higgs o el hipotético inflatón. Estos campos actúan sobre lo que se entiende tradicionalmente como masa, y pueden hacer aparecer efectos extraños sobre el mismísimo espacio-tiempo (como es la aparición de una fuerza repulsiva que aumenta linealmente con el volumen del espacio).
 |
| Una posible explicación para la materia y energía oscura |
En cualquier caso, lo importante del asunto es señalar que las matemáticas del Modelo Estándar permiten la existencia de más partículas fundamentales y más interacciones de las descritas hasta el momento. Sería, groso modo, tan "sencillo" como añadir y/o modificar miembros algebraicos en la estructura de la ecuación del lagrangiano.
Universos paralelos.
Y por fin llegamos a lo que se pretendía tratar desde un inicio en esta entrada: las matemáticas del Modelo Estándar también permiten de la existencia de uno (o varios) Universos que convivan de manera simultánea pero independiente con el nuestro. Sería éste el caso si la realidad contuviese campos cuánticos independientes (grafos inconexos); es decir, si existiesen otros grupos de campos cuánticos (partículas) sin interacción alguna entre sí (ni siquiera gravitatoria). Es decir, que muy bien podría existir un paquete independiente de campos cuánticos similares a los de nuestro día a día, pero con la particularidad de que no interaccionan con ninguno de nuestros bosones portadores de fuerza (ni siquiera con el gravitón).
Una manera sencilla de visualizar lo que acabamos de decir es suponer que existe de manera paralela a los campos descritos en el Modelo Estándar una especie de negativo inconexo de partículas y fuerzas. Tendríamos así las mismas partículas materiales y portadoras de fuerza pero no tendrían conexión ni interacción alguna con las de nuestro "mundo". Es decir, que no habría ningún punto de encuentro ni afectación entre estos campos y los del Modelo Estándar. ¡Tendríamos así "mundos" paralelos conviviendo en la misma región del espacio-tiempo! Y cada Universo tendría sus eventos causales y sus "seres" (fenómenos) autónomos. En estos hipotéticos (y posibles) mundos paralelos podrían incluso existir seres inteligentes como nosotros, los cuales habrían dado a sus campos cuánticos y fuerzas otros nombres, e incluso podrían sospechar de la existencia de nuestro Universo, como estamos nosotros haciendo aquí con el suyo.
Pero hay que dejar claro que esta tesis que defendemos no se limita a la posible existencia de uno o unos pocos Universos paralelos conviviendo literalmente con el nuestro, sino que debemos recalcar la posibilidad de que exista una infinidad de ellos todos actuando a la vez de manera concurrente pero desconectada. De hecho, esta idea podría servir de soporte al multiverso matemático del que nos habla el famoso físico Max Tegmark en su obra "Nuestro Universo matemático". Miles de billones de diversas estructuras matemáticas todas sucediendo en el mismo instante pero inconexas entre sí. Una infinidad de mundos paralelos donde únicamente aquellas estructuras con la complejidad necesaria para albergar vida consciente contendrá seres capaces de preguntarse por la propia estructura matemática que los sustenta (sus propiedades y su comportamiento fenoménico).
¡Es sorprendente que la física moderna permita (e incluso favorezca) la posibilidad de este tipo de hipótesis!
jueves, 16 de julio de 2020
Eterno retorno
"Al mundo me trajeron sin mi consentimiento
y los ojos abrí con sorpresa infinita,
partiré después de reposarme un tiempo
sin saber la razón de mi entrada y salida." (Omar Jayam)
Si hay algo que me eriza el pelo de terror es la idea del eterno retorno. Y si me aterra, es porque la física moderna parece precisamente que apoya la viabilidad de la mismo. Es decir, que en principio la cosmología y la física de partículas parecen favorecer la propuesta que nos dice que todos los sucesos; los mismos acontecimientos, se repiten eternamente en el mismo orden tal cual ocurrieron, sin ninguna posibilidad de variación. De esta forma, se asume que todo lo ocurrido y lo que ocurre en el universo, ocurrió ya y será así hasta el fin de los tiempos.
En este sentido nos habla, por poner un ejemplo; el famoso físico Max Tegmark en su obra "Nuestro Universo matemático". Y aunque no es el único, por supuesto, que habla en este sentido; mereciendo la pena señalar quizás en este sentido a otro autor brillante: Brian Greene y su trabajo "La realidad oculta", Max lo hace de manera ejemplar y clara: la física fundamental conocida hasta el momento parece apoyar con fuerza la hipótesis del multiverso. De hecho, la propuesta del multiverso es hoy día aceptada por gran parte de la comunidad científica, siendo muchas las variantes posibles para el mismo. En este sentido Max Tegmark esquematiza el asunto con cuatro tipo de multiversos que sirven de cajón de sastre donde poder meter y ordenar todas las propuestas que se barajan. Sin embargo, la idea del actual artículo no es describir estas variaciones, sino simplemente señalar que todos estos posibles multiversos comparten una cosa en común: como efecto colateral implican la realidad física del eterno retorno. Y esto es, con perdón, jodidamente aterrador.
En su obra "La gaya ciencia", Friedrich Nietzsche se plantea respecto al concepto de eterno retorno que no sólo son los acontecimientos los que se repiten, sino también los pensamientos, sentimientos e ideas, vez tras vez, en una repetición infinita e incansable. En su aforismo 341 nos dice así:
341. El peso más pesado
"¿Cómo te sentirías si un día o una noche un demonio se deslizara furtivamente en la más solitaria de tus soledades y te dijera: “Esta vida, tal como la estás viviendo ahora y tal como la has vivido [hasta este momento], deberás vivirla otra vez y aún innumerables veces. Y no habrá en ella nunca nada nuevo, sino que cada dolor y cada placer, cada pensamiento y cada suspiro y todo lo indeciblemente pequeño y grande de tu vida deberá volver a ti, y todo en el mismo orden y la misma secuencia – e incluso también esta araña y esta luz de la luna entre los árboles, e incluso también este instante y yo mismo. ¡El eterno reloj de arena de la existencia se invertirá siempre de nuevo y tú con él, pequeña partícula de polvo!”?
¿Acaso te lanzarías al suelo rechinando los dientes y maldecirías al demonio que te hablara de esa forma? ¿O has vivido alguna vez un instante extraordinario, en el que hubieras podido responderle: “¡Eres un dios y nunca he oído algo más divino!”?
Cuando un pensamiento así se apoderase de ti, te metamorfosearía, tal como eres, o tal vez te trituraría; ¡la pregunta sobre cualquier cosa “¿quieres esto otra vez y aún innumerables veces?” se impondría sobre tu actuar como el peso más pesado! O, [podríamos preguntarnos], ¿qué tan bien dispuesto debes estar hacia ti mismo y hacia la vida para no desear ninguna otra cosa que no sea esta última, eterna confirmación, este sello?"
Y ciertamente, si algún demonio nos hablase de este modo, todos rechinaríamos los dientes maldiciendo. Y se engaña, o es un necio, el que piense que se alegraría de saber de ésta realidad. Es más, precisamente el Superhombre (Übermensch) del que nos habla Nietzsche es aquel "mesías" que algún día sería capaz de aceptar esta eterna maldición con alegría. Huelga decir que tal Übermensch es un inefable ideal, probablemente irrealizable. Nuestra existencia en el absurdo mundo sinsentido (objetivo) es ya dura de soportar una única vez, pero se convierte en una total pesadilla si nos obligaran a repetir la misma durante toda una eternidad. ¿Quién puede haber vivido una vida tan plena como para desear repetir la misma, tal cual, una infinidad de veces sin cambiar nada en absoluto? ¿Cómo desear ver una misma película de cine una y otra vez, sin poder modificar lo más mínimo sin acabar desquiciado más pronto que tarde?
Seamos sinceros con nosotros mismos: en un Universo donde vivimos pendientes de qué será lo que vaya finalmente a matarnos (cáncer, virus, accidente,...), padeciendo y luchando a diario, sufriendo y padeciendo por nosotros y los nuestros, tropezando una y otra vez con la misma piedra; corriendo con vehemencia realizando tareas absurdas y repetitivas como si fuésemos hormigas obreras, la peor noticia que podrían darnos es aquella que nos dice que no sólo vamos a vivir esta existencia una única vez, sino una infinidad de veces. Existencias clonadas, repeticiones cinematográficas; una tragicomedia un billón de veces proyectada en donde los actores siempre deben hacer lo mismo sin alternativa.
Porque, como dijo Omar Jayam, a este mundo fuimos lanzados sin consentimiento, y no vemos además razón objetiva alguna para nuestros actos diarios; padecemos porque así viene determinado por la termodinámica que nos dio forma, y sobrevivimos porque la evolución así lo dicta. Pero entre la condena de deber ser una vez, y la atrocidad de obligarnos a ser del mismo modo una eternidad de veces hay un enorme abismo. No se me ocurre destino más terrorífico: el culmen de la crueldad y el sadismo natural.
Así pues, ¡roguemos todos y supliquemos clemencia al mundo! ¡Imploremos con fuerza porque la existencia sea única!
miércoles, 8 de julio de 2020
Sobre la inmunidad al SARS-CoV-2
Hablando sobre la inmunidad frente al nuevo coronavirus:
Se conoce muy mucho la duración de la inmunidad de todos los coronavirus que causan en humanos resfriados (https://www.medrxiv.org/content/10.1101/2020.05.11.20086439v2.full.pdf)
Resultado: la inmunidad no llega al año en casi ningún caso (la cosa queda entre 6 meses y 1 año mayormente). Caso aparte para el SARS y el MERS que dejan inmunizado algo más: entre un año y dos años. Pero claro, el SARS y el MERS causan casi siempre en cuadros severos que es lógico que generen más protección. El SARS-CoV-2 causa mucho caso leve y asintomático por lo que la inmunidad adquirida debe parecerse más a la de sus "hermanos": HCoV-229E, HCoV-NL63, HCoV-OC43 y HCoV-HKU. Y como digo, se sabe que la inmunidad adquirida para estos virus no llega al año casi nunca. Estos estudios sobre la inmunidad adquirida frente a todos los coronavirus que afecta a humanos NO son halagüeñas.
Y el hecho de que los anticuerpos generados para el SARS-CoV-2 se sepa que decaen tan pronto es cierto que no es algo concluyente, pero apunta a que tampoco vamos a quedar protegidos mucho más de un año (siendo generosos).
Y sobre la capacidad de mutación del SARS-CoV-2 pues para ejemplo un botón:
"El cambio en la letra 23.403 del genoma modifica las instrucciones para fabricar la espícula, que ahora presenta un nuevo aminoácido, la glicina, en la posición 614 de esta proteína. Este matiz podría potenciar la infectividad del virus…"
En menos de un año de vida ya ha logrado cambiar a cepas capaces de hacer ésto. Me pregunto como puede afectar esta mutación a las (¿obsoletas?) vacunas en proceso de pruebas...
Si unimos esta inmunidad limitada a la baja exposición actual al virus (donde en España menos del 5% ha estado en contacto con él), volvemos al famoso paper de Harvard que nos describe la dinámica probable que llevará este virus a convivir con nosotros durante varios años:
La gráfica que parece hoy día más probable es la siguiente (línea negra para el SARS-CoV-2 y roja y azul para otros coronavirus causantes del resfriado):
Esta gráfica en concreto se basa en los siguientes valores para los parámetros más importantes del modelo: (A) χ 3X = 0.3, χ X3 = 0, 1 / σ 3 = 40 semanas, f = 0.2.
- χ 3X = 0.3, χ X3 = 0, indica que en este escenario hay muy poca inmunidad cruzada entre los Betacoronavirus del resfriado común y el SARS-CoV-2. Es decir, que pillar un resfriado no implicaría tener mucha menos probabilidad de pillar COVID19.
- 1 / σ 3 = 40, implica una corta duración (40 semanas) de inmunidad contra el SARS-CoV-2 una vez pasada la enfermedad: es decir, los anticuerpos generados no nos otorgan mucha protección conforme pasan los meses. Obviamente no se estima inmunidad permanente para este escenario.
- f = 0.2, implica poca variación estacional. En este caso, el SARS-CoV-2 se vería relativamente poco afectado por los cambios ambientales de humedad y temperatura.
Hace unos meses predije que la salud de nuestra civilización iba a depender de varios factores que eran desconocidos por aquel entonces. Ahora ya se conoce un poco más sobre el asunto:
1) Conocer cuánto dura la inmunidad (memoria) hacia el SARS-CoV-2 y cuánta seroprevalencia existe actualmente (lo que determinará la relación infectados/muertos: letalidad, y lo lejos o cerca que estamos de la inmunidad de grupo). También conocer si esta inmunidad adquirida es eficiente y suficiente para no volver a infectarse del virus aunque sea de manera más leve.
La reinfección parece claramente posible. Siendo la protección inmune probable muy similar a la de sus hermanos: HCoV-229E, HCoV-NL63, HCoV-OC43 y HCoV-HKU (Referencia: https://www.medrxiv.org/content/10.1101/2020.05.11.20086439v2.full.pdf). Esto es: entre 6 meses y un año para toda persona que pasara la información de manera no severa, y de entre un año y dos años para aquellos que la pasaron severamente.
2) Cómo afecta los cambios de temperatura y humedad al virus.
Parece que no afecta tanto la temperatura y humedad como el hecho de que en tiempos de frío la gente se reúne más en espacios cerrados. Por lo tanto, parece que el factor estacional no es demasiado importante per se.
3) Conocer si es posible realizar una vacuna eficiente, barata y fácil de producir en masa; y de ser posible, para cuándo estaría al alcance de 7.000 millones de personas.
Pues aún no se sabe si las vacunas en desarrollo son viables y si protegen de manera eficiente sobre el virus. Lo que sí existe es un peligro claro de que queden obsoletas antes incluso de su pase a producción. Ya existe de hecho una reciente cepa con cambios estructurales en la espiga quizás suficientes para que varias de éstas vacunas no sean efectivas (si es que lo eran). En cualquier caso, hasta mediados/finales del 2021 no habrá posiblemente una vacuna al alcance de toda la población mundial.
4) Determinar si la tasa de mutación de este virus de ARN monocatenario positivo, una vez se vea bajo presión evolutiva (ya sea debido a que se logre vacuna o inmunidad de grupo "natural"), le permitirá safarse con facilidad o no de esta barrera inmune creando nuevas cepas o cambios significativos (como es capaz de hacer la gripe, por ejemplo, o incluso otros coronavirus hermanos, de cuyos resfriados no se libra casi nadie año tras año por mucho que se inmunice la gente de ellos).
No sólo ya ha demostrado ser capaz, sino que lo ha hecho incluso sin una presión evolutiva importante de fondo: ¡en menos de un año de vida!
No pinta nada bien la cosa, aunque todavía hay que confirmar todos estos datos con más profundidad.
Suscribirse a:
Comentarios (Atom)











