"El gran arquitecto parece ser un matemático; a aquellos que no saben matemáticas les resulta realmente difícil sentir la profunda belleza de la naturaleza." (Richard P. Feynman)
A comienzos del siglo XX el mundo de la física recibió un par de revoluciones que vendrían a trastocar completamente nuestra percepción humana del mundo. En concreto hablamos de la relatividad y la física cuántica. Pero mientras que la primera dejaba aún en pie ciertas concepciones de nuestro sentido común, el mundo cuántico vino a destruir por completo nuestro sentido de la realidad.
En esta entrada vamos a intentar explicar (para dummies) algunos aspectos de este asombroso comportamiento del mundo microscópico. Lo haremos sin introducir una sóla ecuación, de la manera más cualitativa y simple posible.
Pero antes de nada, y aunque sea de perogrullo, comentar que la mecánica cuántica apareció gradualmente durante el pasado siglo en un intento por explicar el reino de los fenómenos extraordinariamente pequeños: es decir, aquellos que no se podían "ver" u observar de una manera tradicional. Veamos qué es lo que aquellos científicos se encontraron:
Indeterminación en la trayectoria.
Si disparamos una pistola, podemos seguir el recorrido de la bala (por ejemplo de 9 mm) hasta que finalmente alcance una diana colocada en la pared. Existen cámaras especiales de hecho capaces de seguir el recorrido de la bala a cámara superlenta durante todo su trayecto.
Sin embargo, cuando se "dispara" un objeto subatómico (cuyo "tamaño" se puede aproximar grosso modo al rango del femtometro: 0,0000000000001 mm), ocurre que la trayectoria de este ente NO se puede seguir sin alterar completamente sus propiedades físicas.
Es decir, que la bala de 9 mm recibe de continuo el impacto de billones de fotones (partículas de luz) que rebotan en ella hasta llegar a la cámara superlenta que los recibe y procesa para mostrarnos de manera certera la posición y el camino que la bala va siguiendo. Pero dada la enorme diferencia entre la "gran" masa de la bala y la relativa diminuta energía de los fotones, el proyectil sigue todo su camino sin apenas verse perturbado por dichos impactos.
Sin embargo, si procedemos del mismo modo a lanzar fotones para "ver" y seguir la trayectoria de objetos microscópicos de tamaños (energía-masa) equivalentes a los del propio fotón, el resultado esta vez es distinto, puesto que la posición y la trayectoria de la partícula a seguir se verá muy (muy) afectada por esta medición nuestra. Es como sin lanzaramos balas de 9mm para detectar la trayectoria de otras balas de 9mm: el resultado sería que la bala no llevaría su dinámica normal y acabaría en cualquier sitio, probablemente destrozada (muy perturbada).
Pues bien: esta era (y es) la situación en el mundo microscópico. NO podemos seguir la trayectoria efectiva de estos objetos minúsculos sin perturbar su estado hasta el punto de que lo que finalmente medimos no tiene nada que ver con lo que habría ocurrido sin ese intento nuestro por seguir su rastro. ¡Y no hay nada que hacer al respecto!
Indeterminación en el impacto final.
Pero bueno, a pesar de todo aún tenemos la "diana" al final del trayecto. Eso es lo que pensaron los científicos de principios del siglo pasado. Así que se pusieron a investigar qué ocurría con la distribución en los impactos (interacciones) de estos objetos diminutos.
En cuanto comenzaron los experimentos en este sentido aparecieron nuevos problemas: se dieron cuenta de que no había manera de predecir dónde iba a impactar un objeto microscópico una vez "disparado". Y daba igual con cuánta precisión se preparasen los experimentos y con cuánto énfasis se pretendiese utilizar siempre las mismas condiciones iniciales, el resultado final parecía impredecible (recordemos que en física clásica un experimento que se repita siguiendo las mismas condiciones iniciales siempre dará el mismo resultado final -con cierto pequeño margen de error práctico-).
No había manera. Tras un gran número de repeticiones sin duda se observaban ciertos patrones en los impactos (mediciones), pero por mucho que se intentase parecía en principio imposible predecir dónde concretamente iba a impactar un objeto subatómico concreto: siempre se observaban desviaciones y comportamientos inesperados.
La cosa se complica.
Inicialmente se supuso (como algo lógico) que esta doble indeterminación era un problema práctico y no teórico: es decir, que tales objetos minúsculos poseían un estado de movimiento muy bien definido (i.e., que seguían una trayectoria equivalente al de la bala de 9 mm que usamos antes como ejemplo), de manera que el hecho de no se pudiese determinar con precisión la zona de impacto de una partícula se debía, pensaron los científicos, a que su pequeño tamaño haría que se viera perturbada en su camino por gran cantidad de otros fenómenos (moléculas en el aire circundante, etc.). En otras palabras, que del mismo modo en que no se podía seguir su trayectoria sin modificar a la misma (como vimos arriba), no se podía determinar su lugar preciso de impacto por el mismo motivo; dado que no importa con cuánto tacto se pretendiese replicar las mismas condiciones para el experimento siempre habría una gran cantidad de parámetros ("ocultos") que no podían controlar.
Pero entonces ocurrió lo inesperado. Algo que hizo trizas el sentido común de ese cerebro nuestro evolucionado por completo dentro del mundo macroscópico: el realismo tradicional se vino abajo. Veamos qué sucedió:
Se procedió a realizar el experimento de Young, más conocido como el experimento de la doble rendija, utilizando electrones y otras partículas materiales. Grosso modo, este experimento consiste en disparar elementos sobre una pared con dos aberturas ("agujeros") colocando una "diana" detrás de dicha pared. De este modo, en el caso de las balas de 9 mm la diana mostrará sólo los impactos de los proyectiles que lograron pasar por una de las dos aberturas. Así que el resultado observado tras disparar muchas balas es siempre similar al siguiente
Por lo tanto era de esperar (todos los esperaban) que el resultado del experimento anterior tras lanzar un chorro, por ejemplo de electrones, mostrase en la"diana" una distribución muy similar a la anterior mostrada para las balas de 9 mm (quizás con un ángulo de impacto mayor dado que las partículas todavía se verían más perturbada que las balas en su trayecto tras pasar la abertura hasta llegar a la "diana").
Sin embargo, los investigadores (atónitos) descubrieron que el patrón de impactos no se parecía en nada a lo esperado, mostrando siempre que se repetía este experimento con cualquier tipo de partícula (e incluso con objetos mayores como átomos completos) algo similar a lo siguiente:

La cara de los científicos de la época sería un cuadro cuando vieron este panorama. ¿Pero qué narices estaba pasando allí? Se habría esperado cualquier cosa menos este patrón de impactos tan extraño (incluso una completa aleatoriedad perturbativa se habría asimilado mejor).
Enseguida los físicos se pusieron manos a la obra para pretender explicar este resultado. Y una de las primeras hipótesis propuestas fue la de que, de alguna manera, el beam (el haz de electrones) estaba interfiriendo consigo mismo de alguna manera tras pasar las aberturas. Así que se repitió de nuevo el experimento, pero esta vez lanzando una sola partícula cada diez segundos. Sin embargo al cabo de un tiempo (y tras varios miles de impactos)...¡el patrón acabó siendo el mismo!

Consternados, lo siguiente que hicieron fue coger el aparato y modificarlo tapando una de las dos rendijas:
Y ahora sí, cuando se procedía a realizar el experimento con una sola rendija abierta se encontraba el patrón esperado por el sentido común (el mismo mostrado por las balas). Es decir, que si sólo había una rendija abierta se eliminaba esa extraña interferencia que daba lugar al asombroso patrón observado antes con dos rendijas abiertas:

La explicación.
Ante estos hechos los físicos estaban absolutamente desconcertados. Con una rendija todo parecía seguir los dictados del sentido común, pero al abrir la segunda el patrón de impactos pasaba a mostrar una extraña figura donde se observaba un patrón de zonas donde no acontencía ningún impacto y otras zonas donde sí ocurrían...¡y eso a pesar de que se lanzaban las partículas de una en una!
La única explicación posible pasaba por abandonar el prejuicio del realismo tradicional: después de todo parecía que las partículas no eran esas balas en miniatura que se había supuesto desde el principio. ¡Debían ser "otra cosa"! Algo distribuido (esparcido) por el espacio y capaz de interferir consigo mismo!
Y resulta que el único fenómeno conocido en la naturaleza capaz de presentar tal comportamiento es el de una onda. Así pues el mundo microscópico debía estar compuesto por entes ondulatorios. No había más alternativa. Unos entes microscópicos dispersos en el espacio que debían presentar el efecto ondulatoria de difracción, lo que llevaría a esa interferencia "consigo mismo" observada durante su trayecto a la "diana" tras las rendijas. El efecto propuesto sería algo similar a lo siguiente:
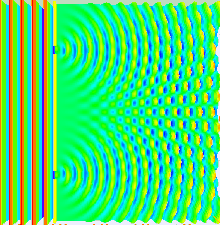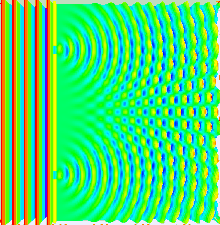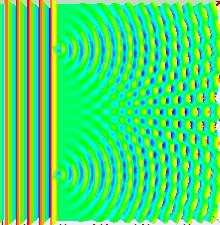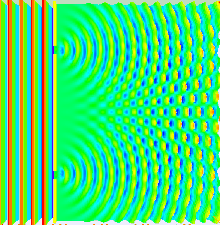
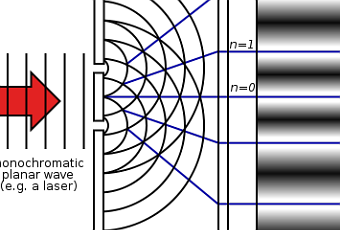
Todo esto implicaba que cuando se lanzaba un electrón, en realidad se lanzaba una onda plana (y NO una bala pequeñita) que tras pasar por la rendija producía difracción e interactuaba consigo misma (debido a los picos y valles de la ondas) de manera que las ondas llegaban a la "diana" con más "fuerza" en algunos lugares que en otros (habiendo partes de la "diana" que no presentaba ningún impacto -zonas oscuras- debido a que allí una cresta y un valle coincidían y se aniquilaban). El sentido común se había venido abajo.
¿Ondas de qué?
En la naturaleza observamos distintos tipos de ondas: ondas sonoras, ondas de fluidos, ondas sísmicas, etc., ¿pero con qué tipo de sustancia o sustrato podíamos identificar estas "ondas de electrones"? Una onda de agua en un estanque, por ejemplo; está compuesta por el movimiento del conjunto de billones de moléculas de agua (H2O) siguiendo una dinámica concreta que finalmente produce el proceso de difracción pero, ¿qué sentido tiene decir que una sóla molécula de H2O es por sí misma una onda y al pasar por una (doble) rendija produce difracción e interferencia consigo misma? No parecía desde luego algo fácil de digerir.
Seguimos con la indeterminación.
Más aún. A pesar de que esta identificación del electrón como una onda plana dispersa en el espacio (en oposición a la idea del electrón como una pequeña bola o bala con posición y trayectoria bien definida) es capaz de dar cuenta de los patrones de impacto obverdados con una y con dos rendijas abiertas, y cuando se disparaba un electrón tras otro de manera independiente...¡todavía no había manera de determinar y prever con certeza a priori donde concretamente iría a parar un electrón concreto tras su disparo! Lo más que se podía hacer era observar la densidad de impactos en las líneas de la "diana" y concluir a posteriori que donde más claras eran esas líneas más probable sería que acabase impactando allí un nuevo electrón cualquiera.
Por lo tanto, a pesar de nuestra incapacidad para prever con certeza dónde iría a parar el siguiente electrón, sabíamos que éste posiblemente iría a parar a una de las zonas más claras de la "diana" (donde en el pasado más impactos se recibió).
Ondas de probabilidad.
Así que finalmente se tuvo que relacionar de este modo el patrón de impactos con un patrón de probabilidad, puesto que se podía observar claramente que había zonas que parecían más probables que otras a la hora de recibir impactos (algunas zonas literalmente con probabilidad igual a cero).
Este hecho supuso además una respuesta implícita a la pregunta que nos hicimos anteriormente: ¿qué tipo de onda es esa "onda del electrón"? ¡Pues "simplemente" una onda de probabilidad! El hecho es que las franjas de impactos en el experimento de la doble rendija es consecuencia directa de la naturaleza ondulatoria del electrón individual (que produce difracción e interfiere consigo mismo con sus valles y crestas), y por lo tanto es esta misma naturaleza ondulatoria la que determina la distribución de probabilidad final en los impactos de la diana. Por lo tanto podemos interpretar (al cuadrado matemático) de esta "onda-electrón" directamente como una onda de probabilidad que se dispersa y se mueve por el espacio.
Por lo tanto finalmente nació así una nueva disciplina llamada mecánica cuántica, la cual se encargaba precisamente de ayudarnos a calcular de manera precisa y para cualquier sistema microscópico (del cual el experimento de la doble rendija es sólo un pequeño ejemplo) la distribución de probabilidad de observar algún resultado concreto.
Resumen.
Partimos de la (errónea) premisa de que el mundo microscópico era una versión en miniatura del mundo macroscópico tal y como lo observamos nosotros (realismo tradicional o de sentido común). Pero pronto nos dimos cuenta de que no hay manera de "ver" o seguir la trayectoria de tales entes puesto que son tan pequeños que cualquier intento por detectarlos destruye y altera completamente su estado de movimiento y localización. Tampoco había (ni hay) manera de poder predecir con certeza dónde acabará un objeto microscópico por mucho que se refinen y controlen las condiciones iniciales experimentales; habiendo incluso ocasiones donde la partícula acaba (impacta) en lugares que clásicamente (macroscópicamente) no tienen sentido alguno (están prohibidos).
Para más inri aparecieron experimentos donde una partícula parecía interferir consigo misma de una manera ondulatoria, pero al mismo tiempo no era fácil interpretar qué tipo de onda puede generar un único objeto (y no una colección de objetos, como ocurre con todas las gotas de un lago ondulante). Esta "onda-partícula" además parecía determinar de algún modo la distribución de probabilidad en el estado final (el impacto, medición, u observable) de los experimentos.
Así pues, y tras un shock intelectual, nuestro sentido común como decimos se vino abajo: el mundo microscópico es muy extraño, y su parecido con nuestra realidad cotidiana es, siendo generosos, una mera metáfora. Las partículas no son esas bolitas pequeñitas que pensábamos, ni tienen una posición y momento bien determinados, ni siguen trayectorias fijas que podamos seguir, ni dan como resultado estados que podamos predecir con certeza.
Cuando hablamos de objetos en el rango de los 0,0000000000001 mm, el mundo es radicalmente distinto. A esta escalas dichos entes "materiales" vemos que "son" en realidad ondas de probabilidad: entidades matemáticas en forma de ondas senoidales y cosenoidales cuyo cuadrado determinan la densidad de probabilidad para el observable en el estado final de cualquier sistema microscópico. Unas ondas que normalmente se aglutinan y se mezclan en el espacio-tiempo, de manera que el estado y la disposición de varias partículas se ven así a veces también entrelazadas y superpuestas hasta que algún acto de medición las devuelve a la individualidad (ondulatoria).
Por lo tanto, a estas escalas, en el mundo todo son ondas de probabilidad dispersas espacialmente: ondas que como decimos se mezclan, se superponen, se entrelazan, ondas en resumen que con sus picos y valles determinan la distribución de probabilidad para cualquier evento a medir.
Lanzamiento de dados.
Pero todavía nos queda una última extrañeza más antes de terminar con el artículo: el famoso lanzamiento de dados que tanto disgustó a nuestro amigo Einstein.
Hemos visto que todo a escalas subatómicas funciona en base a ondas de probabilidad que se esparcen y mueven en el espacio (de manera similar a las ondas de un estanque) siguiendo la famosa ecuación de Schrödinger; pero la esencia natural todavía nos guarda una sorpresa más:
Puesto que en el laboratorio no vemos en ningún momento ondas sino "impactos" (mediciones que son arbitrarias pero que como ya vimos siguen una clara distribución de probabilidad), entonces de algún modo debe ocurrir que estas (invisibles e indetectables) ondas "materiales" de probabilidad deben colapsar: es decir, que deben dejar de ser ondas y convertirse en "otra cosa"; algo tangible a lo que físicos llaman un observable.
- Vamos a concretar todo lo visto hasta ahora utilizando de nuevo el experimento de la doble rejilla donde se lanza un electrón cada 10 segundos:
Cuando la "pistola" crea y lanza un electrón, no dispara en realidad una bolita diminuta sino una onda plana de probabilidad. Esta onda plana (que en realidad se dispersa en las tres dimensiones por entre todo el Universo, ahí es nada) pasa a la vez por las dos rendijas produciendo el conocido efecto de difracción y la consiguiente interacción entre valles y picos, lo cual perturba la onda de probabilidad entre la abertura y la "diana" (como un estanque cuando se le tira una piedra). Finalmente esta onda(-electrón) de probabilidad que permea ya todo el espacio (todo el Universo, recuerda) con cierta altura en cada posición x indica (al elevarse al cuadrado la misma) la probabilidad de que el electrón acabe ("impacte") en cierta posición concreta (el observable). En el caso de la "diana" tras las dos aberturas, es también el cuadrado de la altura en la onda de probabilidad lo que indica cuán probable es que se produzca un impacto en cada posición x de la "diana". Ese "impacto" en sí (de acontecer) supone un tipo de medición, por lo que la onda de probabilidad se ve obligada a colapsar, desapareciendo de todo el Universo y transformándose en "otra cosa": un observable (en este caso un punto fosforescente en una pantalla). Este colapso supone además la elección natural (no se sabe todavía cómo) de un resultado (estado) final concreto de entre todos los posibles (siendo los posibles estados aquellos que tenían una probabilidad no nula justo antes del proceso de medición). Es decir, que el mundo a la hora de colapsar cualquier onda de probabilidad realiza el equivalente a "tirar un dado" para seleccionar así un estado final concreto dentro del abanico (ponderado) de opciones posibles.
Por lo tanto el patrón que muestra la "diana" tras el experimento de la doble rendija supone la sucesión de colapsos en la onda de probabilidad lanzada desde la "pistola" cada 10 segundos, por lo que es normal que se presente ese patrón de interferencia tan concreto puesto que es en el fondo una proyección de la mismísima onda de probabilidad que no podemos "ver" de ninguna manera más que de forma indirecta tras las mediciones en la distribución de probabilidad de un sistema concreto de estudio.
La mecánica cuántica.
Fueron precisamente estas observaciones que os he descrito las que se fueron formalizando matemáticamente durante la primera mitad del siglo XX (por científicos de gran renombre) hasta dar lugar finalmente a lo que hoy día se conoce como mecánica cuántica. Una teoría probabilista y no local que choca frontalmente con nuestro sentido común, y a la cual todavía no se la sabe interpretar bien más allá de los buenos (buenísimos) resultados matemáticos que consigue en cuanto a su respaldo experimental.
Pero debe quedar claro que nadie sabe realmente cómo funciona en esencia el mundo natural a estas escalas (por mucho que las matemáticas sean certeras): nadie comprende por qué el mundo microscópico funciona a base de este tipo de ondas, la razón de toda esa indeterminación que vimos al principio (que formalmente toma luego la forma del principio de indeterminación de Heisenberg), nadie sabe si realmente las partículas(-ondas) siguen "físicamente" trayectorias como tal o si simplemente "saltan" de aquí para "allá" según las matemáticas que las determinan. Y tampoco nadie sabe que son "realmente" en sí estas ondas "materiales" de probabilidad (invisibles e indetectables), nadie comprende por qué se produce el colapso de estas extrañas ondas, por qué es el cuadrado matemático de dichas ondas lo que guía la realidad, ni tampoco se sabe cómo selecciona el mundo en esencia ese aleatorio (pero ponderado) resultado final observable (¿cómo tira el Universo los dados?). Es decir, que fuera de las matemáticas todo sigue siendo en general duda y controversia.
- Nota para quisquillosos:
El proceso histórico descrito en esta entrada (para dummies) no es 100% preciso, y me he tomado ciertas libertades literarias para intentar explicar de la forma más asequible posible las propuestas de la mecánica cuántica. Así pues hay estudios anteriores, posteriores, intermedios y la línea histórica en general no es rigurosa. No obstante la idea es que cualquier persona sin conocimientos previos pueda entender la enorme extrañeza oculta tras los postulados de la física cuántica ;).
¿Es cierto que, si se pone un detector en una rendija (o en las dos), el patrón desaparece?
ResponderEliminar